EML 5060Analysis in Mechanical Engineering Fall 1999
Test 1 Van Dommelen (dommelen@eng.famu.fsu.edu) Due 9/3/99

Hand in the solution to this test on 9/3/99 (5% of your final grade). If your performance is insufficient, you will need to hand in a corrected version; however, only your initial grade counts. Please note: This test must have been accepted before exam 1, or you also receive a 0 grade for exam 1. Read carefully. And look it up.

Neatly draw the graph of the following function, showing the locations of 0 and $\pm 1$ on each axis. Give the derivative. Indicate non-principal values as a broken line. Make sure that you give enough of the curves to clearly demonstrate all features:

$$2x-2 \qquad \qquad \qquad \qquad x^2 + 1 \qquad \qquad \qquad \qquad x^4 - x^2$$

$$\sin(x)\qquad \qquad \qquad \qquad \arcsin(x)\qquad \qquad \qquad \qquad \sinh(x)$$

$$\cos(x)\qquad \qquad \qquad \qquad \arccos(x)\qquad \qquad \qquad \qquad \cosh(x)$$

$$\tan(x)\qquad \qquad \qquad \qquad \arctan(x)\qquad \qquad \qquad \qquad \tanh(x)$$

$$\ln(x)\qquad \qquad \qquad \qquad e^x\qquad \qquad \qquad \qquad \tan(x^2)$$

Find (include any integration constants and absolute signs):

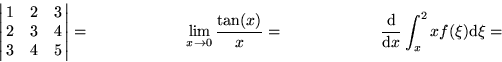
$$\int x^{-2} {\rm d} x= \qquad \qquad \qquad \int_1^2 x^{-2} {\rm d} x = \qquad \qquad \qquad \int_1^x \xi^{-2} {\rm d} \xi =$$

$$\int {{\rm d} x \over x} = \qquad \qquad \qquad \int {1\over... ...m d} x = \qquad \qquad \qquad \int {1\over 1 + x^2} {\rm d} x =$$

$$\int \ln(x) {\rm d} x = \qquad \qquad \qquad \int x e^x {\rm d} x = \qquad \qquad \qquad \int x e^{x^2} {\rm d} x =$$

$$\left\vert \matrix{ 1 & 2 & 3\cr 2 & 3 & 4\cr 3 & 4 & 5} \ri... ... \qquad {{\rm d} \over {\rm d} x} \int_x^2x f(\xi) {\rm d}\xi =$$

$$2 + 1 + 0 - 1 -2 -3 -4 \ldots -99 -100 = \qquad \qquad\qquad... ...+ e^{1} + e^{0} + e^{-1} + e^{-2} + e^{-3} + e^{-4} + \ldots =$$

$${\rm Solve: }\quad{{\rm d} y\over {\rm d} x} = y \qquad y(1)=1$$