EML 5060 Analysis in Mechanical Engineering I 12/14/18
Closed book Van Dommelen 10-12 noon

Solutions should be fully derived showing all intermediate results, using class procedures. Show all reasoning. Bare answers are absolutely not acceptable, because I will assume they come from your calculator (or the math handbook, sometimes,) instead of from you. You must state what result answers what part of the question. Answer exactly what is asked; you do not get any credit for making up your own questions and answering those. Use the stated procedures. Give exact, fully simplified, answers.

One book of mathematical tables, such as Schaum's Mathematical Handbook, may be used, as well as a calculator, and a handwritten letter-size formula sheet.

1. Background: Vibrating systems are typically described by differential equations. For small amplitides, these can often be solved exactly.

   Question: Using undetermined coefficients and the other class procedures, including clean up, solve the forced and damped vibrating system,
   

   $$y'' + 4 y' + 8 y = 16 t^2 + 4 + 8e^{-2t} \qquad y(0)=3,\quad y'(0)=-2$$
   
   

   Solution.

2. Background: The Laplace transform is a primary way to study the stability and evolution of linearized dynamical systems, because it turns them into algebraic systems.

   Question: Use the Laplace transform to find the solution for the following damped vibrating system that is put into motion using a constant force applied over a finite time interval:
   

   $$\ddot x + 4 \dot x + 8 x = F(t) \qquad F(t) = 8 \mbox{ if ... ...T; \quad F(t) = 0 \mbox{ if } t > T \qquad x(0)=\dot x(0)=0$$
   
   
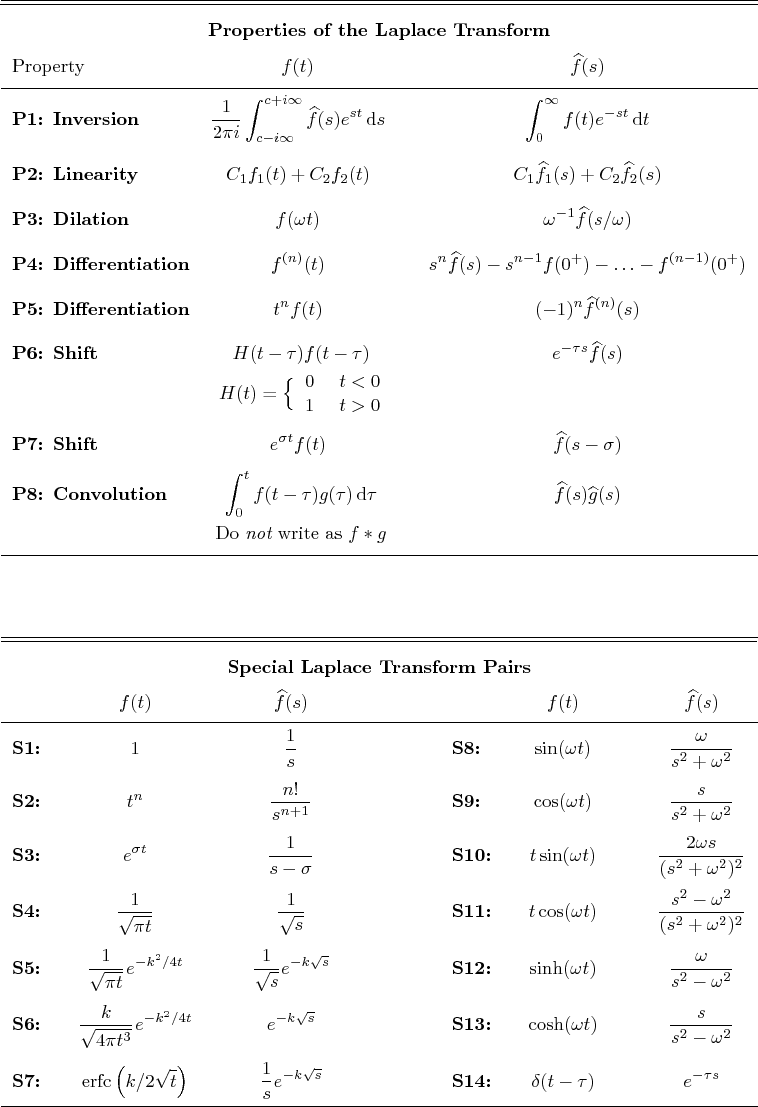
   A table of Laplace transforms is attached. Everything not in this table must be fully derived showing all reasoning. P1 may not be used, and the convolution theorem only where it is unavoidable. Do not use any complex numbers in your analysis (besides $s$.) You can only use one Laplace transform table entry at each step (except P2), and its table number must be listed. No funny (discontinuous) functions or stars in your answers.

   Solution.

3. Background: Nonlinear dynamical systems often cannot be solved analytically. However, valuable qualitative understanding can often be obtained using critical (stationary) point analysis.

   Question: Show that the dynamical system
   

   $$\dot y = 5 \sinh(x) - 2y \qquad \dot y = -\sinh(x) + 4y$$
   
   
   gives rise to only one stationary point problem,
   
   $$\left(\begin{array}{c} \dot x \\ \dot y \end{array}\right) ... ...ray}\right) \left(\begin{array}{c} x \\ y \end{array}\right)$$
   
   

   Solve this system using the class procedures. Then very accurately and neatly draw a complete set of solutions lines, covering all areas, near the stationary point like shown in class. Make sure angles and slopes are right. Classify the stationary point. Could the stationary point analysis be qualitative wrong? Explain all.

   Solution.

Table 1: Properties of the Laplace Transform. ($k,\tau,\omega>0$, $n=1,2,\ldots$)