By signing below, I certify that I will not communicate
in any way about the exam before 7 pm:
Signature: Date:
EML 5060 Analysis in Mechanical Engineering 12/11/20
Closed book Van Dommelen 3-5 pm
Solutions should be fully derived showing all intermediate
results, using class procedures. Show all reasoning.
Bare answers are absolutely not acceptable, because I will assume they
come from your calculator (or the math handbook, sometimes,) instead
of from you. You must state what result answers what part of the
question. Answer what is asked; you do not get any credit for
making up your own questions and answering those. Ask if
clarification of what is asked is needed. Use the stated procedures.
Give exact, fully simplified, answers where possible.
One book of mathematical tables, such as Schaum's Mathematical
Handbook, may be used, as well as a calculator, and a handwritten
letter-size formula sheet.
Write on the front side of the pages only.
- Background: Differential equations of second order are
common in engineering because of dynamics. Below is an equation for
the dynamics of a stable system with generic forcing.
Question: Solve the ordinary differential equation
with 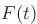 an arbitrary function of
an arbitrary function of 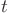 , using variation of
parameters.
, using variation of
parameters.
Note: Since you cannot do the integrals for the coefficients
analytically without knowing function 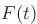 , write them as
, write them as
where 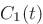 is function
is function 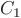 evaluated at time
evaluated at time 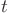 and
and
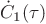 is function
is function 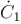 evaluated at time
evaluated at time 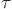 ,
and similar for
,
and similar for 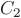 . This trick allows you to show the
integration constants explicitly. Work out the final expression for
. This trick allows you to show the
integration constants explicitly. Work out the final expression for
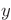 completely.
completely.
Solution.
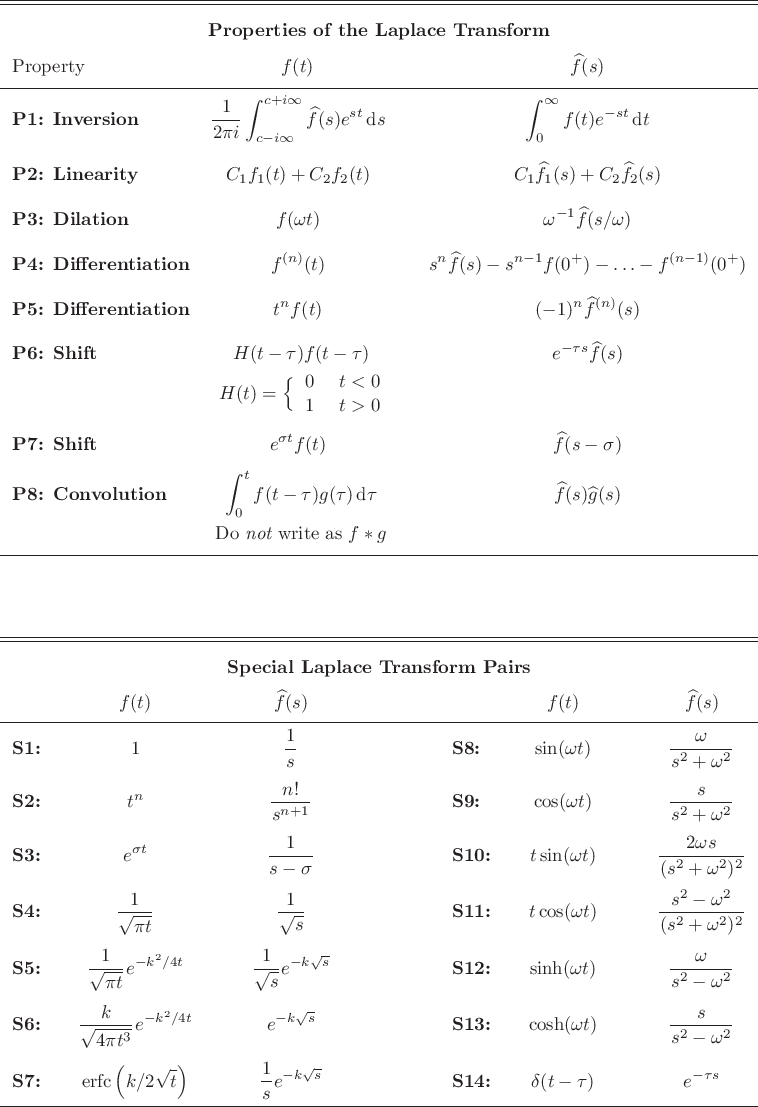
- Background: The Laplace transform is a primary way to
study the stability and evolution of linearized dynamical systems,
because it turns them into algebraic systems.
Question: Use the Laplace transform to solve the following
damped vibrating system with generic forcing:
A table of Laplace transforms is attached. Everything not in this
table must be fully derived showing all reasoning. P1 may not be
used, and the convolution theorem only where it is unavoidable. Do
not use any complex numbers in your analysis (besides 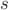 .) You can
only use one Laplace transform table entry at each step
(except P2), and its table number must be listed. No funny
(discontinuous) functions in your answers.
.) You can
only use one Laplace transform table entry at each step
(except P2), and its table number must be listed. No funny
(discontinuous) functions in your answers.
Solution.
- Background: Since any system of differential equations can
be reduced to a first order system, all you really need to know is
how to solve these systems.
Question: Solve using the class procedures for systems of ODE,
including variation of parameters:
In particular, find the solution for the initial condition
Clean up your answer.
Note: if you do not make algebraic mistakes, the algebra should be
fairly simple.
Solution.
![]() , write them as
, write them as