


Up: Return
EML 5060 Analysis in Mechanical Engineering 10/18/94
Closed book Van Dommelen 9:00-9:50 EST
Show all reasoning and intermediate results leading to your answer.
One book of mathematical tables, such as Schaum's Mathematical Handbook,
may be used.
Jack Tsai may use one English or English-Chinese dictionary.
- 1.
- For the truss shown below, the tension forces in the bars satisfy the
equations
-T1 + T2 = 0
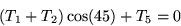
- T3 +T4 = 0
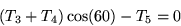
If the vector of unknowns is token to be (T1,T2,T3,T4,T5)T,
give the matrix representing the above equations.
Reduce to echelon form. From the echelon form,
show that the bars may be under tension or
compression, even though there are no external forces.
The only thing we can be sure of are the ratios of the tension
forces in the bars. Determine these.
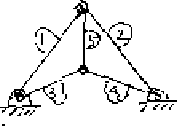
- 2.
- Consider the two masses suspended by springs below.
Newton's equations of motion are:

We will assume that k=m=1.
If we look for solutions of the form

we find that
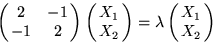
Find the two values of 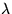 for which such motion is possible.
Also find the corresponding ratio of X1/X2, i.e. of x1/x2.
for which such motion is possible.
Also find the corresponding ratio of X1/X2, i.e. of x1/x2.
- 3.
- For the 2 by 2 matrix shown in question 2,
evaluate the matrix
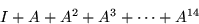
Do not use laborious procedures that are error prone.



Up: Return
'Author: Leon van Dommelen'
![]()
![]()
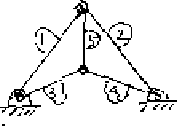
![]()
![]()
![]()
![]()
![]()
![]()
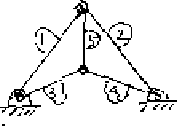
![]()
![]()
![]()
![]()