Up: Return
EML 5060 Analysis in Mechanical Engineering 12/13/95
Closed book Van Dommelen 12:30-2:30pm
Show all reasoning and intermediate results leading to your answer.
One book of mathematical tables, such as Schaum's Mathematical Handbook,
may be used.
- 1.
- (33 points).
Consider steady supersonic flow at a Mach number 3.33 under a 45 degree
angle with the x-axis. Small changes in the horizontal velocity
component u(x,y) satisfy
4 uxx + 10 uxy + 4 uyy = 0.
Find new coordinates 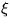 and
and 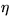 such that the equation satisfied
by
such that the equation satisfied
by 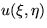 takes the form
takes the form
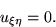
Use this result to show that the solution for u must be of the form
u(x,y) = f(2x-y)+g(2y-x),
where f and g are arbitrary functions.
Solution
- 2.
- (33 points).
Solve heat conduction in a semi-infinite bar which is initially
at zero temperature. Heat is removed through the end at a
rate which increases linearly in time:
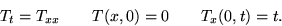
Note: you will probably not succeed in simplifying the
final result for u.
Solution
- 3.
- (34 points).
Solve steady heat conduction in a quarter circle.
The straight sides are insulated:
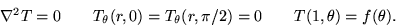
Write the solution in terms of 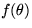 .Also, if
.Also, if 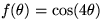 , what is u?
Solution a
Solution b
, what is u?
Solution a
Solution b
Up: Return
![]()
![]()
![]()
![]()
![]()
![]()