| Additional notes on linear algebra |
|
© Leon van Dommelen |
|
4 LU Theorem
If you put minus the multipliers in a Gaussian elimination without
partial pivoting in a lower triangular matrix 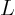 , with values 1 on
the main diagonal, then
, with values 1 on
the main diagonal, then
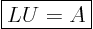 |
(1) |
That is the 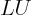 theorem.
theorem.
After 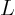 and
and 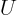 have been found through Gaussian elimination, you
can solve
have been found through Gaussian elimination, you
can solve 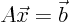 for any given right hand side vector
for any given right hand side vector 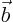 as follows: The system to solve is according to the theorem
as follows: The system to solve is according to the theorem 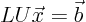 . Temporarily call
. Temporarily call 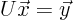 . Solve
. Solve 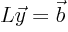 using simple forward substitution. With
using simple forward substitution. With 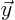 now known,
now known, 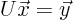 can be solved using back substitution as before:
can be solved using back substitution as before:
 |
(2) |
In case partial pivoting was needed, remember the row order
interchanges you did and do the same interchanges with the
coefficients of 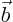 before solving as above. You also need to
do the row exchanges on the forming matrix
before solving as above. You also need to
do the row exchanges on the forming matrix 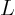 while doing the GE.
while doing the GE.
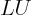 will then be the matrix
will then be the matrix 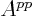 , equal to matrix
, equal to matrix 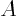 except with
its rows in the final order produced by all the row interchanges.
except with
its rows in the final order produced by all the row interchanges.
For large 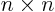 matrices the number of computer
matrices the number of computer
operations
(defined as 1 multiplication and 1
addition) to find 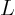 and
and 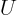 is approximately
is approximately 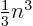 . After
that, to find a
. After
that, to find a 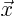 given a
given a 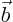 takes only about
takes only about 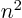 operations.
operations.
Some warnings. Normally speaking:
- Never ever use Cramer's rule for anything but the tiniest of
matrices. Multiplying out a determinant takes about
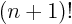 operations, which is gigantically larger than
operations, which is gigantically larger than 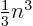 for
everything except the tiniest
for
everything except the tiniest 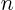 . Not to mention the possible
round-off error growth with so many operations. And the risk of
overflow and underflow (i.e. numbers getting outside the range that
they can be stored on a computer.)
. Not to mention the possible
round-off error growth with so many operations. And the risk of
overflow and underflow (i.e. numbers getting outside the range that
they can be stored on a computer.)
- If you find the inverse matrix
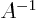 , you can simply find any
, you can simply find any
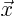 as
as 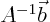 . But that is normally a bad idea. One
reason is that it takes
. But that is normally a bad idea. One
reason is that it takes 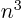 operations to find
operations to find 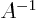 , three
times more than to find
, three
times more than to find 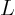 and
and 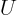 . And to evaluate
. And to evaluate 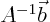 still takes
still takes 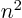 operations. Also the additional operations tend
to increase round-off error, [1].
operations. Also the additional operations tend
to increase round-off error, [1].
- A band matrix is a matrix in which the nonzero elements
are restricted to a relatively narrow band around the main diagonal.
Never ever use an LU decomposition library routine designed for a
full matrix to solve a system with a band matrix. The waste in
storage and computer effort to store all these zeros, and compute
with them, would be gigantic. Use an LU decomposition subroutine
designed for a band matrix.
- Never ever find the inverse of a band matrix if you can help it.
The inverse will be a full matrix. However,
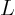 and
and 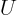 will still
be band matrices. (Partial pivoting may increase
will still
be band matrices. (Partial pivoting may increase 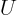 a bit to
outside the band of
a bit to
outside the band of 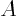 , by up to the width of
, by up to the width of 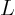 .)
.)
![]() , with values 1 on
the main diagonal, then
, with values 1 on
the main diagonal, then
![]() and
and ![]() have been found through Gaussian elimination, you
can solve
have been found through Gaussian elimination, you
can solve ![]() for any given right hand side vector
for any given right hand side vector ![]() as follows: The system to solve is according to the theorem
as follows: The system to solve is according to the theorem ![]() . Temporarily call
. Temporarily call ![]() . Solve
. Solve ![]() using simple forward substitution. With
using simple forward substitution. With ![]() now known,
now known, ![]() can be solved using back substitution as before:
can be solved using back substitution as before:
![]() before solving as above. You also need to
do the row exchanges on the forming matrix
before solving as above. You also need to
do the row exchanges on the forming matrix ![]() while doing the GE.
while doing the GE.
![]() will then be the matrix
will then be the matrix ![]() , equal to matrix
, equal to matrix ![]() except with
its rows in the final order produced by all the row interchanges.
except with
its rows in the final order produced by all the row interchanges.
![]() matrices the number of computer
matrices the number of computer
![]() and
and ![]() is approximately
is approximately ![]() . After
that, to find a
. After
that, to find a ![]() given a
given a ![]() takes only about
takes only about ![]() operations.
operations.