6 Finding null spaces and solution spaces

To find the null space of a matrix, reduce it to echelon form as described earlier. To refresh your memory, the first nonzero elements in the rows of the echelon form are the pivots. Solve the homogeneous system by back substitution as also described earlier. To refresh your memory, you solve for the pivot variables. The variables without pivots cannot be solved for and become parameters with arbitrary values in the null space, multiplying “basis vectors”. The coefficients inside the basis vectors come from the solved variables or from writing trivialities.

For example, if your unknowns are $(x_1,x_2,x_3,x_4,x_5,x_6)$ and your echelon matrix is

$$\left( \begin{array}{cccccc} 0 & 2 & 4 & 6 & 8 & 6 ... ...0 & 2 & 4 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{array} \right)$$

then the last equation is trivial and you get from the third

$$2 x_5 + 4 x_6 = 0 \quad\Longrightarrow\quad x_5 = -2 x_6$$

then from the second

$$x_4 = 0$$

then from the first

$$2 x_2 + 4 x_3 + 6 (0) + 8 (-2 x_6) + 6 x_6 = 0 \quad\Longrightarrow\quad x_2 = - 2 x_3 + 5 x_6$$

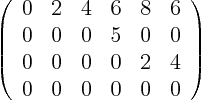
To get the null space (i.e. the full set of vectors $(x_1,x_2,x_3,x_4,x_5,x_6)$ that produce zero when premultiplied by the original $A$), the variables $(x_1,x_3,x_6)$ without pivots go in the right hand side as arbitrary constants that can be anything:

$$\mbox{null space:}\qquad \left( \begin{array}{c} x_1 \... ...n{array}{c} 0 5 0 0 -2 1 \end{array} \right)$$

The coefficients for the pivot variables $(x_2,x_4,x_5)$ in the vectors in the right hand side come from the solved equations, and those for $(x_1,x_3,x_6)$ from trivialities.

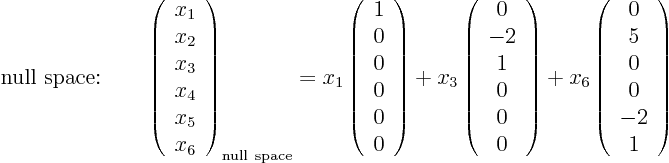
To get a basis for the null space, you can use the constant vectors in the right hand side:

$$\mbox{a basis of the null space:}\qquad \left( \begin{... ...n{array}{c} 0 5 0 0 -2 1 \end{array} \right)$$

(By definition any vector in the null space is a linear combination of the above three vectors. And it is easy to see that the three are linearly independent.)

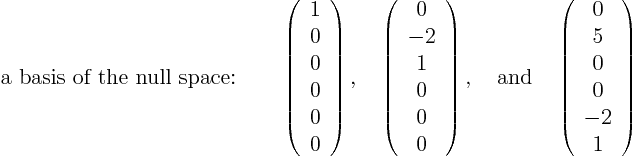
If the above basis would contain fractions, you should consider multiplying them by some nonzero constants to clean up. Note that that will of course affect the given expression for the null space.

To find a solution space is almost the same as finding the null space, except that you will use an augmented matrix to include the given nonzero right hand side. The right hand side will produce an additional vector in the solution space that is not multiplied by any unknown. Therefore the solution space is not a vector space (assuming that the given right hand side is not zero) and has no basis.