2 7.20m, §2 P.D.E. Model

**Figure 2:** Heat conduction in a bar.
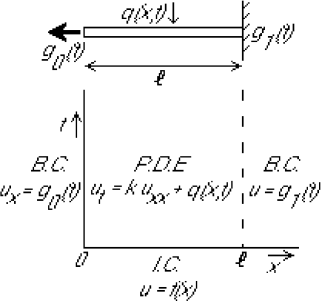$\begin{figure}\begin{center} \leavevmode \epsffile{figures/1.eps} \end{center}\end{figure}$

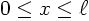
Finite domain $\bar \Omega$ : $0\le x \le \ell$
Unknown temperature
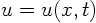
Constant 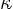$\kappa$ , so a linear constant coefficient PDE.
Parabolic
Inhomogeneous
One initial condition
One Neumann boundary condition
One Dirichlet boundary condition
All of 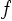, , 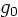, 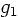and 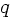are given functions.

We would like to use separation of variables to write the solution in a form that looks roughly like:

$\begin{displaymath} u(x,t) = \sum_n u_n(t) X_n(x) \end{displaymath}$

Here the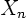

would be the eigenfunctions. The

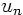cannot be eigenfunctions since the time axis is semi-infinite. Also, Sturm-Liouville problems require boundary conditions at both ends, not initial conditions.

However, eigenfunctions must have homogeneous boundary conditions, so if 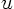was written as a sum of eigenfunctions, it could not satisfy the given inhomogeneous boundary conditions. Fortunately, we can apply a trick to get around this problem.