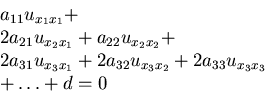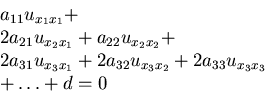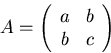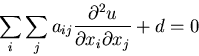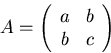2nd Order

The general n-dimensional second order quasilinear equations is:

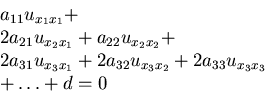
Its coefficients can be placed into a symmetric matrix A, just like those of a quadratic form can be.

Example:

a u_xx + 2b u_yx + c u_yy + d = 0

The matrix A is here:

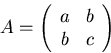
In index notation, the n-dimensional equation can be written as:

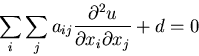
where 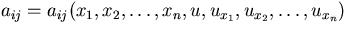is a symmetric matrix and .

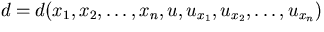Classification is based on the eigenvalues of A:

• parabolic if any eigenvalues are zero; otherwise:
• elliptic if all eigenvalues are the same sign;
• hyperbolic if all eigenvalues except one are of the same sign;
• ultrahyperbolic, otherwise.

Exercise: Figure out whether that is consistent with what we defined for the two-dimensional case,

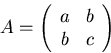
• hyperbolic if b²-ac>0.
• parabolic if b²-ac=0.
• elliptic if b²-ac<0.