Characteristic Coordinates

Characteristic coordinates are coordinates so that a' and c' vanish:

Finding characteristic coordinates:

Vanishing of a' requires that satisfies

while for c' to vanish,

Note that and must satisfy the exact same equation, but they must be different solutions to be valid independent coordinates.

To solve the equation for ( goes the same way), divide by :

and note that, from your calculus or thermo,

So the lines of constant should satisfy the ODE

We can achieve this by taking to be the integration constant in the solution of this ODE!

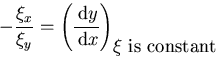
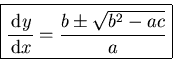
By taking the other sign for the square root, you can get a second independent coordinate .

Bottom line, to get characteristic coordinates, solve the plus and minus sign ODE above, and equate the integration constants to and .

Notes:

1.

Since integration constants are not unique, the characteristic coordinates are not. But the lines of constant and are unique, and are called characteristic lines or characteristics.

2.

Elliptic equations do not have characteristics, and parabolic ones only a single family.

Application to the wave equation:

u_tt - a² u_xx = 0

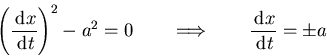
Since d' remains zero:

Hence the D'Alembert solution:

u = f₁(x-at)+f₂(x+at),

which is a right travelling 'wave' plus a left travelling one. Example 4.10 figures out what f₁ and f₂ are in terms of given initial displacement u and velocity u_t at the initial time.