Up: Introduction
Previous: §2 Formulae
For linear, constant coefficient equations, rotate the coordinate
system to the principal axes of A:
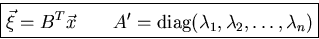
provided that B consists of the orthonormal eigenvectors of A.
Our equation simplifies to
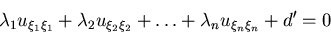
Notes:
- 1.
- If A is not constant, we must select a point P for which we
determine the eigenvectors. The new A' will then only be diagonal at
the point P.
- 2.
- If A is not constant, trying to set B at every point
equal to the eigenvectors of the A at that point will not usually
work since it requires n2 equations to be satisfied by the
n components of
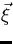 .
. - 3.
- If we do not normalize the eigenvectors,
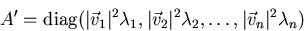
Up: Introduction
Previous: §2 Formulae
![]()
![]()
![]()