Next: 7.37, §6 Total
Up: 7.37
Previous: 7.37, §4 Eigenfunctions
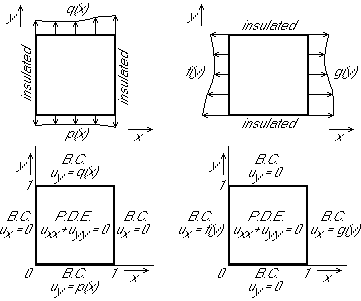
Expand all variables in the problem for u in a Fourier series:
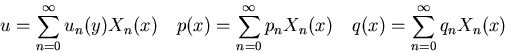
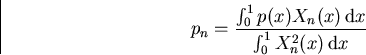
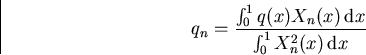
Remember that the expression you find for the integrals in the bottom,
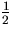 , does not work for n=0, in which case it turns out to
be 1.
, does not work for n=0, in which case it turns out to
be 1.
Fourier-expand the PDE uxx + uyy = 0:
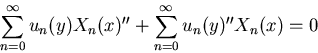
Because of the Sturm-Liouville equation in the previous section
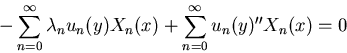
giving the ODE
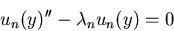
or substituting in the eigenvalue
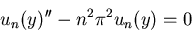
Fourier-expand the BC uy(x,0) = p(x):
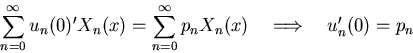
Fourier-expand the BC uy(x,1) = q(x):
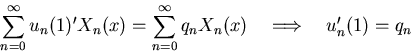
Solve the above ODE and boundary conditions for un. It is a constant
coefficient one, with a characteristic equation
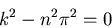
Caution! Note that both roots are the same when n=0. So we need
to do the n=0 case separately.
For 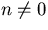 the solution is
the solution is
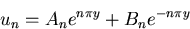
The boundary conditions above give two linear equations for An and
Bn:
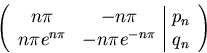
whic are best solved using Gaussian elimination. Rewriting the
various exponentials in terms of sinh and cosh, the solution for the
Fourier coefficients of u except n=0 is:
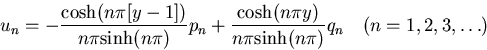
For n = 0 the solution of the ODE is
u0 = A0 + B0 y
Put in the boundary conditions to get equations for the integration
constants A0 and B0:

Oops! We can only solve this if
p0 = q0
Looking above for the definition odf those Fourier coefficients,
we see we only have a solution if
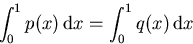
Unfortunately, these two integrals will normally not be equal!
Also, A0 remains unknown. No problem! Students will explain and
fix the problem.
Next: 7.37, §6 Total
Up: 7.37
Previous: 7.37, §4 Eigenfunctions


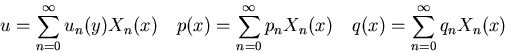
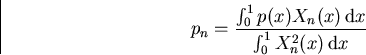
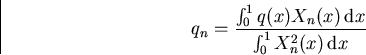
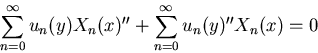
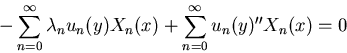
![]()
![]()
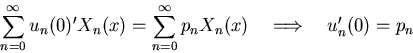
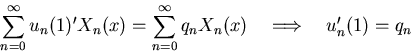
![]()
![]() the solution is
the solution is
![]()
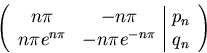
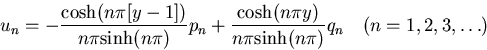
![]()
![]()