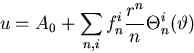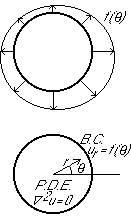
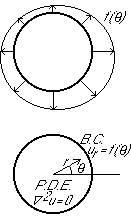
We will again expand all variables in the problem in a Fourier series.
Let's start with the function ![]() giving the outflow through
the perimeter.
giving the outflow through
the perimeter.
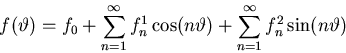
Since ![]() is supposedly known, we should again be able to find
its Fourier coeficients using orthogonality. The formulae
are as before.
is supposedly known, we should again be able to find
its Fourier coeficients using orthogonality. The formulae
are as before.
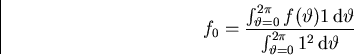
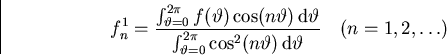
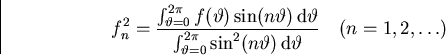
Since I hate typing big formulae, allow me to write the Fourier series
for ![]() much more compactly as
much more compactly as
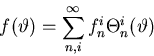
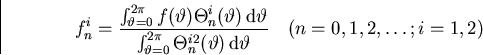
Next, let's write the unknown ![]() as a compact Fourier
series:
as a compact Fourier
series:
![]()
We put this into P.D.E. ![]() :
:
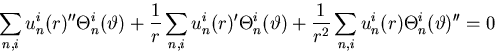
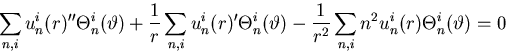
We get the following ODE for uin(r):
![]()
r2 uin(r)'' + r uin(r)' - n2 uin(r) = 0
This is not a constant coefficient equation. Writing down a characteristic equation is no good.Fortunately, we have seen this one before: it is the Euler equation. You solved that one by changing to the logaritm of the independent variable, in other words, by rewriting the equation in terms of
![]()
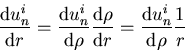
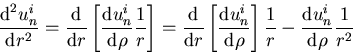
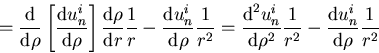
The ODE becomes in terms of ![]() :
:
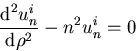
![]()
![]()
Now both ![]() as well as r-n are infinite when
r=0. But that is in the middle of our flow region, and the
flow is obviously not infinite there. So from the `boundary
condition' at r=0 that the flow is not singular, we conclude that
all the B-coefficients must be zero. Since r0=1, all coefficients
are of the form Ain rn, including the one for n=0.
as well as r-n are infinite when
r=0. But that is in the middle of our flow region, and the
flow is obviously not infinite there. So from the `boundary
condition' at r=0 that the flow is not singular, we conclude that
all the B-coefficients must be zero. Since r0=1, all coefficients
are of the form Ain rn, including the one for n=0.
Hence our solution can be more precisely written
![]()
Next we expand the boundary condition ![]() at r=1 in a Fourier series:
at r=1 in a Fourier series:
![]()
n Ain = fin
For n=0, we see immediately that A0 can be anything, but we need f0=0 for a solution to exist! According to the orthogonality relationship for f0, this requires:
![]()
For nonzero n:
![]()