- Finish finding the derivatives of the unit vectors of the
spherical coordinate system using the class formulae. Then finish
1st Ed p160 q47, 2nd Ed p183 q47, as started in class, by finding
the acceleration. Note that the metric indices
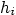 for spherical
coordinates are in mathematical handbooks. Also,
for spherical
coordinates are in mathematical handbooks. Also,
- Express the acceleration in terms of the spherical velocity
components
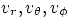 and their first time derivatives,
instead of time derivatives of position coordinates. Like
and their first time derivatives,
instead of time derivatives of position coordinates. Like
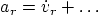 , etc. This is how you do it in fluid mechanics,
where particle position coordinates are normally not used. (So, get
rid of the position coordinates with dots on them in favor of the
velocity components.)
, etc. This is how you do it in fluid mechanics,
where particle position coordinates are normally not used. (So, get
rid of the position coordinates with dots on them in favor of the
velocity components.)
- The Laplace equation
where subscripts indicate derivatives, is an elliptic equation. Such
a steady-state equation needs boundary conditions at all points of
the boundary. For example, one properly posed problem on the unit
square is
Identify 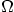 ,
, 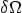 , and the type of each boundary
condition (Dirichlet, Neumann, Robin).
, and the type of each boundary
condition (Dirichlet, Neumann, Robin).
The wave equation
is an hyperbolic equation. The above boundary conditions are
not properly posed for the wave equation. (as you will see in
a later homework.) For the wave equation, one of the coordinates
must be time-like, and must have initial conditions instead of
boundary conditions. The following initial and boundary conditions
are properly posed for the wave equation,
For each of the four, determine whether it is an IC or BC, and if
so, what kind of BC. The time-like coordinate is not normally
included in the domain 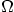 . Under those conditions, identify
. Under those conditions, identify
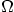 and
and 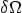 .
.
Check that the following proposed solution satisfies the PDE and all
BC/IC of both the Laplace and wave equation problems:
However, it is a valid solution to only the wave equation. Explain
for what qualitative reason is it not a valid solution to the
Laplace equation.
- The Laplace equation problem as written in the previous
question does not have a simple solution. However, if you distort
the domain into a quarter circle as in
then the solution is simple. Identify and draw 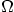 for the
above problem. Identify the type of each boundary condition. Also
draw
for the
above problem. Identify the type of each boundary condition. Also
draw 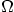 and the boundary conditions for the Laplace problem of
the previous question, and then compare the two problems. Are they
very similar?
and the boundary conditions for the Laplace problem of
the previous question, and then compare the two problems. Are they
very similar?
Now verify, by checking PDE and boundary conditions, that the
correct solution to the modified problem is simply
You may want to switch to a different coordinate system to do so.
Plot this valid solutions for the Laplace equation, as well as the
valid solution for the wave equation of the previous question, on
the circle 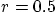 against
against 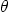 . Comment on whether the change
of a single sign between the wave equation and the Laplace equation
makes any difference for the solution.
. Comment on whether the change
of a single sign between the wave equation and the Laplace equation
makes any difference for the solution.
- 4.18. You are to check that the given
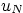 satisfies the given
PDE, the heat equation, and the given boundary conditions. The
given solution is the one you will find using the so-called method
of separation of variables, and normally
satisfies the given
PDE, the heat equation, and the given boundary conditions. The
given solution is the one you will find using the so-called method
of separation of variables, and normally 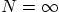 . What is the
type of the boundary conditions? What can you say about the initial
condition that is satisfied?
. What is the
type of the boundary conditions? What can you say about the initial
condition that is satisfied?
- The solution to the wave equation problem of question 3
that you would find using separation of variables is:
Verify the PDE, BC, and IC for this solution. For the first IC, you
will want to look up the sum you get in the “Fourier
series” section of a mathematical handbook, with maybe a
rescaled 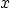 -coordinate.
-coordinate.
Comment whether it would be easy to see the simple form of the
solution from merely looking at the above sum. To make
understanding the solution easier, use the fact that
Describe the two component solutions you get this way in physical
terms.
- The solution to the Laplace equation problem of question 3
that you would find using separation of variables is:
Verify the PDE and BC for this solution.
Next, shed some light on the question why this solution is smooth
for 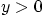 , while the previous solution of the wave equation has a
jump for all
, while the previous solution of the wave equation has a
jump for all 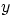 . To do so, first argue that a finite sum of
sines of the form
. To do so, first argue that a finite sum of
sines of the form
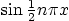 is necessarily a smooth
function of
is necessarily a smooth
function of 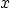 with no jumps or whatever other singularities.
with no jumps or whatever other singularities.
Then show that the coefficients of the sines go to zero much faster
for 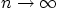 for the solution of the Laplace equation than for
the one of the wave equation. In particular show that for any
positive power
for the solution of the Laplace equation than for
the one of the wave equation. In particular show that for any
positive power 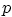 ,
,
while
does not exist for 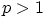 .
.
With such a fast decay of the coefficients of the Laplace equation
solution, the sum is almost finite and singularities are not
possible.
- 2.19b, h. Show a picture of the different regions.
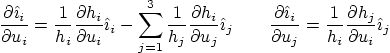
![]() against
against ![]() . Comment on whether the change
of a single sign between the wave equation and the Laplace equation
makes any difference for the solution.
. Comment on whether the change
of a single sign between the wave equation and the Laplace equation
makes any difference for the solution.
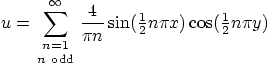
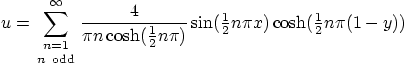
![]() , while the previous solution of the wave equation has a
jump for all
, while the previous solution of the wave equation has a
jump for all ![]() . To do so, first argue that a finite sum of
sines of the form
. To do so, first argue that a finite sum of
sines of the form
![]() is necessarily a smooth
function of
is necessarily a smooth
function of ![]() with no jumps or whatever other singularities.
with no jumps or whatever other singularities.
![]() for the solution of the Laplace equation than for
the one of the wave equation. In particular show that for any
positive power
for the solution of the Laplace equation than for
the one of the wave equation. In particular show that for any
positive power ![]() ,
,