13 04/18 F

1. Continuing the previous homework, substitute $u(x,t)=\sum_nu_n(t)X_n(x)$ into the PDE to convert it into an ordinary differential for each separate coefficient $u_n(t)$. Solve the ODE. Be very careful with one particular case.

2. By writing the initial conditions in terms of the eigenfunctions, identify the integration constants. Write out a complete summary of the solution. Make sure to identify the values of your numbering index in each expression.

3. Reconsider the separation of variables solution you derived. Using some programming language, evaluate the found solution at 101 equally spaced $x$-values from 0 to $\ell$ at time $t=0.25$ and so plot $u$ versus $x$ at that time. Repeat for $t=0.5$. Include at least 50 nonzero terms in the summations. Take $\ell=1$ and $a=1$. Compare with your (or the instructor’s) D’Alembert solution. It should show good agreement. What happens if you only include 10 terms in the summations?

   To help you get started, a Matlab program that plots the solution to problem 7.28 is provided as an example. You need both p7_28.m and p7_28u.m. This program is valid for the PDE and BC solved in class, with the additional data
   

   $$a={\textstyle\frac{1}{2}},\quad \ell={\textstyle\frac{1}{2}... ...n = \frac{1}{(2n-1)^2}, \qquad g(x) = 0 \Rightarrow g_n = 0.$$
   
   
   These may of course not apply for your problem.

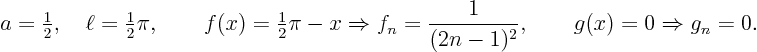
   To run the program, enter matlab and type in p7_28. If you do not have matlab, a free replacement is octave. Or you can use some other programming and plotting facilities.

   Include your code.

4. Solve 7.26, by Laplace transforming the problem as given in time. This is a good way to practice back transform methods. Note that one factor in $\widehat u$ is a simpler function at a shifted value of coordinate $s$.

5. Solve 7.35 by Laplace transform in time. Clean up completely; only the given function may be in your answer, no Heaviside functions or other weird stuff. There is a minor error in the book’s answer.

6. Refer to problem 7.19. Find a function $u_0(x,t)$ that satisfies the inhomogeneous boundary conditions. Define $v=u-u_0$. Find the PDE, BC and IC satisfied by $v$.

7. Find suitable eigenfunctions in terms of which $v$ may be written, and that satisfy the homogeneous boundary conditions. Write the relevant known functions in terms of these eigenfunctions and give the expressions for their Fourier coefficients.