EML 4930/5930 Analysis in M.E. II 02/25/09
Closed book Van Dommelen 9:40-10:30 am
Show all reasoning and intermediate results leading to your answer, or
credit will be lost. One book of mathematical tables, such as Schaum's
Mathematical Handbook, may be used, as well as a calculator and one
handwritten letter-size single formula sheet.
- Parallelogram
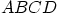 has its corner point
has its corner point 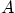 at the origin.
The diagonally opposite point is C.
at the origin.
The diagonally opposite point is C.
- Write the area of this parallelogram in terms of the vectors
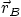 and
and 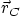 . Clean up.
. Clean up.
- Parallelepiped
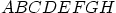 has point
has point 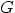 diagonally opposite to
diagonally opposite to
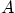 and has
and has 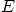 on the same edge as
on the same edge as 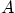 . Write diagonal
. Write diagonal 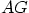 in
terms of
in
terms of 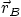 ,
, 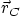 , and
, and 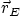 .
.
- Write the volume of the parallepiped
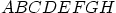 in terms of
in terms of
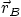 ,
, 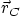 , and
, and 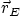 . Clean up.
. Clean up.
- Evaluate all of the above if
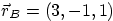 ,
,
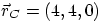 , and
, and
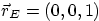 . Clean up.
. Clean up.
Solution.
- A screw thread can be modeled as the spiral
where 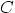 is a constant. This spiral is on the surface of a
circular cylinder of unit radius around the
is a constant. This spiral is on the surface of a
circular cylinder of unit radius around the 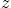 -axis.
-axis.
- Give the unit vector tangential to the curve at a given point.
- Find the curvature and torsion of the spiral.
- Find the unit normal to the plane of the osculating circle and
its radius. Is the center of the circle on the axis of the
cylinder?
Solution.
- Reduce the PDE
to canonical form by rotating the coordinate system. Give the
rotated coordinates in terms of the original ones and the canonical
PDE.
Solution.