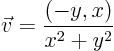3 HW 3

1. 1st Ed: p80, q102, 2nd Ed: p94, q102. Make sure that you find $\phi$ in a mathematically sound way, as discussed in class. No messing around and guessing a solution!

2. (9 points). Modified version of a question in the book. Maxwell’s equations in vacuum are
   
   $$\fbox{$\displaystyle \begin{array}{ccccc} \displaystyle ... ...a \cdot \vec E = 4 \pi \rho & \quad\emph{(d)} \end{array} $}$$
   
   
   Here $\vec E$ is the electric field, $\vec H$ the magnetic field, $\rho$ the charge density (the electric charge per unit volume), $\vec\jmath$ the current density (the current flowing per unit cross sectional area), and $c$ the speed of light, a constant. Consider $\rho$ and $\vec\jmath$ to be given functions of position and time. You need to show that any solution $\vec E,\vec H$ of the above equations is given by scalar and vector potentials $\phi,\vec A$ as described below.

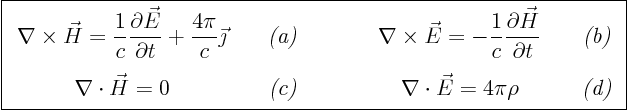
   Procedure to follow:

   1. Explain why there must be a vector potential $\vec A_0$ so that
      
      $$\vec H = \nabla \times \vec A_0$$
      
      

   2. Next define a vector $\vec E_\phi$ by setting
      
      $$\vec E = - \frac{1}{c} \frac{\partial \vec A_0}{\partial t} + \vec E_\phi$$
      
      

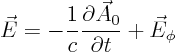
   3. Prove that the $\vec E_\phi$ defined this way is minus the gradient of some scalar potential $\phi_0$. Then the above equation becomes:
      
      $$\vec E = - \frac{1}{c} \frac{\partial\vec A_0}{\partial t} - \nabla\phi_0$$
      
      

   4. Unfortunately, $\vec A_0$ and $\phi_0$ are not unique. We now want, given potentials $\vec A_0$ and $\phi_0$, find modified potentials $\vec A$ and $\phi$. These must still give
      
      $$\fbox{$\displaystyle \vec H = \nabla \times \vec A \quad \... ...partial\vec A}{\partial t} - \nabla\phi \quad \emph{(f)} $}$$
      
      
      However, in addition they must satisfy the famous “Lorenz condition”
      
      $$\fbox{$\displaystyle \nabla\cdot\vec A + \frac{1}{c} \frac{\partial\phi}{\partial t} = 0 \quad \emph{(1)} $}$$
      
      
      (No, there is no t in Lorenz. That is another Lorentz. The Lorenz condition is critical, because it is the only condition that all observers can agree on.) The potentials you need are of the form
      
      $$\vec A = \vec A_0 + \nabla \psi \qquad \phi = \phi_0 - \frac{1}{c} \frac{\partial \psi}{\partial t}$$
      
      
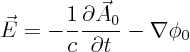
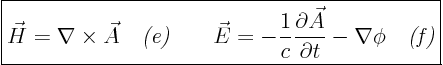
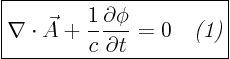
      Prove that in those terms, (e) and (f) above are true regardless of what you take for $\psi$. That is the famous gauge property of the electromagnetic field. It is central to quantum field theory. It defines the electromagnetic field in modern quantum theories, all the rest is derived.
   5. Since you can take $\psi$ whatever you like, you can choose it so that the Lorenz condition (1) is satisfied. Show that this leads to a partial differential equation for $\psi$. (This equation is called an inhomogeneous wave equation. The properties of this equation will be discussed in the second part of the class.)
   6. Now substitute what you got so far into the four Maxwell equations and so find the requirements that $\vec A$ and $\phi$ must satisfy. (I.e. get rid of the electric and magnetic fields in favor of the vector and scalar potentials $\vec A$ and $\phi$.)
   7. How come only one vector equation and one scalar equation are left?
   8. Clean up! You must obtain decoupled equations for the scalar and vector potentials.
   9. Finally, combine (a) and (d) to get a relation between the charge and current densities. (This equation is similar to the continuity equation in incompressible flow and expresses that no charge can be created out of nothing.)

3. 1st Ed: p103, q44, 2nd Ed: p123, q44. (a) Use vector line integration. (b) Do it using Stokes.

4. CHANGE BELOW 1st Ed: p104, q62, 2nd Ed: p124, q62. Do the surface integrals both directly and using the divergence theorem. Make sure to include the flat circle of the cone. Note: in doing the surface integrals directly, you are required to write them down in Cartesian coordinates using the expression for $\vec{n} {\rm d}{}S$ given in class when $F(x,y,z)=0$. After that, switch to polar coordinates to actually do the integration.

5. MODIFIED version of 1st Ed: p132, q50, 2nd Ed: p154, q50. Given
   
   $$\vec v = \frac{(-y,x)}{x^2+y^2}$$
   
   
   1. Evaluate $\nabla\times\vec{v}$.
   2. Also evaluate, presumably using polar coordinates,
      
      $$\int_{\rm I} \vec v \cdot {\rm d}\vec r \qquad \int_{\rm II} \vec v \cdot {\rm d}\vec r$$
      
      
      where path I is the semi circle of radius $r$ going clockwise from $(r,0)$ to $(-r,0)$, and path II is the semi circle of radius $r$ going counter-clockwise from $(r,0)$ to $(-r,0)$.
   3. Explain why the integral over II minus the integral over I is the integral over the closed circle.
   4. Explain why Stokes implies that the closed contour integral should be the integral of the $z$-component of $\nabla\times\vec{v}$ over the inside of the circle.
   5. Then explain why you would then normally expect the contour integral to be zero. That means that the two integrals I and II should be equal, but they are not.
   6. Explain what the problem is.
   7. Do you expect integrals over closed circles of different radii to be equal? Why?
   8. Are they actually equal?
   Now assume that you allow singular functions to be OK, like Heaviside step functions and Dirac delta functions say. Then figure out in what part of the interior of the circle, $\int\!\int\nabla\times\vec{v}\cdot{\hat k} {\rm d}{x}{\rm d}{y}$ is not zero. So how would you describe $\nabla\times\vec{v}$ for this vector field in terms of singular functions?