
 Up: Return
Up: Return
EGN 5456 Homework 5 Fall 1996
-
Solve

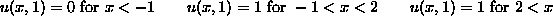
- Draw the solution of the previous question in the
u,x-plane for times t=1, 2, and
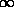 .
.
- Draw the characteristic lines of the partial differential
equation of the previous questions. Indicate along which of these
characteristics the solution is singular.
- If we replace the initial condition in the previous questions
by u(x,1)=f(x) where f is smooth, (eg
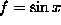 ), will there
ever be singularities in u? Explain.
), will there
ever be singularities in u? Explain.
- One-way vehicular traffic satisfies the continuity
equation of fluid dynamics,

Is this in conservation law form? Is it in divergence form?
- The previous equation can be differentiated out to give

Is this in conservation law form? Is it in divergence form?
- Find a conservation law for any arbitrary finite
road interval
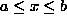 by integrating the differential
conservation law between a and b.
by integrating the differential
conservation law between a and b.
- Explain the conservation law you got in the previous question
physically.
- Plot the characteristics of the traffic equation assuming that
the velocity
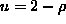 and that the initial density at time t=0 is
given by
and that the initial density at time t=0 is
given by 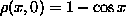 .
.
- Solve the problem of the previous question for
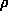 in terms
of
in terms
of 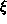 and t, where
and t, where 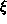 is the starting x-position of the
characteristic at time t=0/
is the starting x-position of the
characteristic at time t=0/
- Plot the car density in the
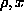 -plane for times t=0,
t=.25 and t=.5.
-plane for times t=0,
t=.25 and t=.5.
- Find the locations and times at which the first car collisions
(shocks) occur.
- The Euler equations of 2D steady, inviscid, nonconducting
two-dimensional flow are:
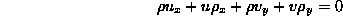



Show that according to the last equation
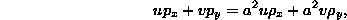
where 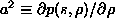 .
.
- Classify the system of the previous question using
the fifth equation instead of the fourth (entropy) one.
- Classify the following system of equations:


- Find and sketch the characteristic lines of the equations of the
previous question.
- Find the compatibility equations equivalent to the system of
equations.
- Find the Riemannian invariants of the compatibility equations
assuming the initial conditions
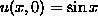 ,
, 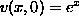 .
.
- From the Riemannian invariants, find the solution u(x,t) and
v(x,t) to the system of P.D.E.s and initial conditions.

 Return
Author: Leon van Dommelen
Return
Author: Leon van Dommelen