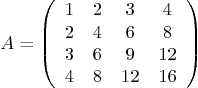
However, your code should work for any value of
If you cannot get this to work, behind your feeble attempts,
just set ![]() manually to the above values to do the rest.
manually to the above values to do the rest.
Show both A and its transpose to verify that A is symmetric.
Now let MATLAB find the eigenvalues and eigenvectors of this matrix.
Then put the last two eigenvectors ![]() and
and ![]() in
separate one-dimensional arrays called eVec3 and
eVec4 and put the last eigenvalue
in
separate one-dimensional arrays called eVec3 and
eVec4 and put the last eigenvalue ![]() in a scalar
variable lam4. Then use eVec4 and lam4
to verify directly that indeed
in a scalar
variable lam4. Then use eVec4 and lam4
to verify directly that indeed ![]() .
Also verify that the lengths of both eVec3 and
eVec4 are one, and that eVec3 is orthogonal to
eVec4.
.
Also verify that the lengths of both eVec3 and
eVec4 are one, and that eVec3 is orthogonal to
eVec4.
- Use the appropriate ez... function to plot the
Folium of Descartes
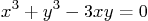
Restrict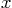 and
and 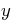 to the range from
to the range from  2 to 2. Use a square
axis system and a grid.
2 to 2. Use a square
axis system and a grid.
- The equation for the lemniscate of Bernoulli is
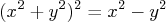
Solve this equation symbolically to give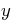 in terms of
in terms of 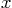 .
Then substitute the value
.
Then substitute the value 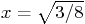 into the solution and see
what you get for
into the solution and see
what you get for 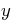 . Show the pretty version of this solution
also. You should get 4 roots, but only two of these roots are
real. Show the two real roots separately as symbolic expressions
y1 and y2. Finally, collect the coefficients of
the powers of
. Show the pretty version of this solution
also. You should get 4 roots, but only two of these roots are
real. Show the two real roots separately as symbolic expressions
y1 and y2. Finally, collect the coefficients of
the powers of 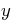 in the symbolic expression
in the symbolic expression
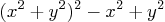
together to see why the Toolbox solves the expression so easily: it is a quadratic equation if you take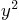 as the unknown!
as the unknown!
- Define a symbolic ratio ratSym as
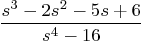
Then show this ratio as a single factored ratio. Also show the partial fraction expansion of the ratio. Give a pretty version of the latter.
Then define a two-dimensional grid for the plate in which the grid
points have these ![]() and
and ![]() -values. Also define an array
forcing for the grid points that is zero for the grid
points in the interior of the plate. For the grid points on the
boundaries of the plate, array forcing should have the
given temperatures on the boundary: For the left hand and bottom
boundaries the temperature is given to be zero, but on the right
hand boundary it is
-values. Also define an array
forcing for the grid points that is zero for the grid
points in the interior of the plate. For the grid points on the
boundaries of the plate, array forcing should have the
given temperatures on the boundary: For the left hand and bottom
boundaries the temperature is given to be zero, but on the right
hand boundary it is ![]() and on the top boundary it is
and on the top boundary it is ![]() . Put
that in array forcing. Then use array forcing in
function SimplePoisson to create the temperature values
TGrid at all the grid points. (Ignore the warning about
CONDEST.)
. Put
that in array forcing. Then use array forcing in
function SimplePoisson to create the temperature values
TGrid at all the grid points. (Ignore the warning about
CONDEST.)
(Note: If you cannot get TGrid right, behind your feeble attempts, put the code
xGrid=zeros(m,n); yGrid=zeros(m,n); TGrid=zeros(m,n);
for i=1:m; for j=1:n
xGrid(i,j)=xVals(j); yGrid(i,j)=yVals(i);
TGrid(i,j)=xVals(j)^2*yVals(i);
end; end
which will produce a fake TGrid good enough for doing
the rest of this question.)
Plot the obtained temperature distribution as a surface with
smoothly varying shading. Label all three axes, the temperature
axis as Temperature
.
Also plot the isotherms (lines of constant temperature) in the ![]() plane. In particular, plot the lines where the temperature is
0.1, 0.2, ..., and 0.9. Label the axes.
plane. In particular, plot the lines where the temperature is
0.1, 0.2, ..., and 0.9. Label the axes.
Use double percent lines and/or figure numbers to ensure that both plots end up in the published pdf file.