Linear interpolation is a way to fill in the ``holes'' in tables. As
an example, if you want to find the saturated pressure of water at a
temperature of 40![]() C you can look in Table B.1.1, (p.674), for
40
C you can look in Table B.1.1, (p.674), for
40![]() C in the first column. The corresponding desired pressure
is then in the next column; in this case, 7.384 kPa. But what if you
want to find the saturated pressure at 38
C in the first column. The corresponding desired pressure
is then in the next column; in this case, 7.384 kPa. But what if you
want to find the saturated pressure at 38![]() C instead of
40
C instead of
40![]() C?
C?
A temperature of 38![]() C is not in the table. You could of course
just ignore the difference between 38
C is not in the table. You could of course
just ignore the difference between 38![]() C and 40
C and 40![]() C, and
still take the saturated pressure to be 7.384 kPa. But that is not
acceptable in this class; it is too inaccurate. To get an accurate
value, you must use linear interpolation. (Though taking the closest
value, 40
C, and
still take the saturated pressure to be 7.384 kPa. But that is not
acceptable in this class; it is too inaccurate. To get an accurate
value, you must use linear interpolation. (Though taking the closest
value, 40![]() C, is of course better than nothing in case you
forgot how to do linear interpolation during an exam.)
C, is of course better than nothing in case you
forgot how to do linear interpolation during an exam.)
Let's introduce a few symbols. Let g be your given value,
38![]() C in this example. Let g1 and g2 be the two closest
approximations to g in the table. A look at Table B.1.1 shows
that the two closest values you can find in the table are 35
C in this example. Let g1 and g2 be the two closest
approximations to g in the table. A look at Table B.1.1 shows
that the two closest values you can find in the table are 35![]() C
and 40
C
and 40![]() C, so in our example g1=35
C, so in our example g1=35![]() C and
g2=40
C and
g2=40![]() C. (The desired value is in between those two, hence
the ``in'' in ``interpolation.'')
C. (The desired value is in between those two, hence
the ``in'' in ``interpolation.'')
Also, let d be our desired value, in our example the saturated
pressure. Let d1 and d2 be the approximate desired values
corresponding to g1 and g2. In our example, Table B.1.1 gives
the saturated pressure at g1=35![]() C to be d1=5.628 kPa and
the saturated pressure at g2=40
C to be d1=5.628 kPa and
the saturated pressure at g2=40![]() C to be d2=7.384 kPa.
Both d1 and d2 are approximations to our desired pressure, but
neither is accurate enough.
C to be d2=7.384 kPa.
Both d1 and d2 are approximations to our desired pressure, but
neither is accurate enough.
The formula for linear interpolation is:
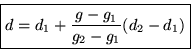
So, in our example, the desired saturated pressure d at 38![]() C
is:
C
is:
![]()
You need two variables to read off the compressed liquid or
superheated vapor tables. In the next example, we will find the
specific volume of steam at a given temperature of 100![]() C and a
given pressure of 20 kPa.
C and a
given pressure of 20 kPa.
Steam (superheated water vapor) is found in Table B.1.3. We have no
difficulty finding the given 100![]() C in that table, but we cannot
find the given pressure of 20 kPa. The closest pressures in the table
are 10 kPa and 50 Kpa.
C in that table, but we cannot
find the given pressure of 20 kPa. The closest pressures in the table
are 10 kPa and 50 Kpa.
So in the linear interpolation formula from the previous section,
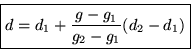
The desired quantity d is now the specific volume at 100![]() C
and 20 kPa. We set the value d1 to the specific volume at g1=10
kPa (and 100
C
and 20 kPa. We set the value d1 to the specific volume at g1=10
kPa (and 100![]() C,) so d1=17.19561 m3/kg according to the
table, and d2 to the specific volume at g2=50 kPa (and
100
C,) so d1=17.19561 m3/kg according to the
table, and d2 to the specific volume at g2=50 kPa (and
100![]() C,) so d2=3.41833 m3/kg.
C,) so d2=3.41833 m3/kg.
Our formula then gives the specific volume at 20 kPa and 100![]() C
as:
C
as:
![]()
You might ask what happens to the last example if neither the given
pressure nor the given temperature is in the table. For example, to
find the specific volume at 20 kPa and 110![]() C, neither 20 kpa
nor 110
C, neither 20 kpa
nor 110![]() C are in Table B.1.4. I do not think we would do this
to you during the exam. But the answer would be to do three linear
interpolations: first interpolate a specific volume at 110
C are in Table B.1.4. I do not think we would do this
to you during the exam. But the answer would be to do three linear
interpolations: first interpolate a specific volume at 110![]() C
and 10 kPa (fill in the 110
C
and 10 kPa (fill in the 110![]() C ``hole'' in the 10 kPa data),
next interpolate a specific volume at 110
C ``hole'' in the 10 kPa data),
next interpolate a specific volume at 110![]() C and 50 kPa (fill in
the 110
C and 50 kPa (fill in
the 110![]() C ``hole'' in the 50 kPa data), and finally linear
interpolate those 110
C ``hole'' in the 50 kPa data), and finally linear
interpolate those 110![]() C values in the same way as we did for
100
C values in the same way as we did for
100![]() C in the previous section.
C in the previous section.
Another problem arises if you try to interpolate the specific volume
of steam at 11 kPa and 50![]() C. You can use the B.1.3 entry for
50
C. You can use the B.1.3 entry for
50![]() C and g1=10 kPa, giving d1=14.86920 m3/kg. But
unfortunately, the 50 kPa data start at 81.33
C and g1=10 kPa, giving d1=14.86920 m3/kg. But
unfortunately, the 50 kPa data start at 81.33![]() C; no 50
C; no 50![]() C
steam at 50 kPa exists. The key to find a second table entry, to give
you g2 and d2, is to recognize that superheated steam ends at
saturation, which is in table B.1.1. You can find the desired second
table entry there; in particular, B.1.1 at 50
C
steam at 50 kPa exists. The key to find a second table entry, to give
you g2 and d2, is to recognize that superheated steam ends at
saturation, which is in table B.1.1. You can find the desired second
table entry there; in particular, B.1.1 at 50![]() C gives a second
pressure g2=12.350 and specific volume d2=12.0318. Which means
that the formula
C gives a second
pressure g2=12.350 and specific volume d2=12.0318. Which means
that the formula
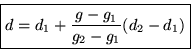
![]()