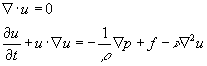
The Taylor-Proudman Theorem in Rotating Fluid Dynamics
George Buzyna
The emphasis of this presentation is on some aspects of rotating fluid dynamics. Several interesting features appear here. We shall examine one of these known as the Taylor-Proudman theorem or condition.
There are many applications of rotating fluid dynamics. Some examples are the general circulation of the atmosphere, large-scale circulation of the oceans, and many rotating systems with fluids in engineering applications.
Much of the fluid dynamics covered in our mechanical engineering curriculum deals with non-rotating situations, i.e. flows in a fixed inertial frame. The governing equations are familiar to us. For an incompressible viscous fluid they are the equations of conservation of mass (continuity equation) and conservation of momentum (the Navier-Stockes equations). In vector notation they are:
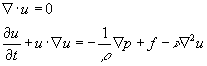
The fluid motion we see in a rotating reference frame is relative to the rotating frame and thus not an inertial reference frame where the above equations of motion are valid. To obtain the equation of motion in a rotating reference frame we must adjust the acceleration terms in the equations.
Recall from dynamics the description for the acceleration of two particles A and B observed from an inertial reference frame. Let the rotating reference frame be attached to point B. The expression for acceleration in vector form is:
The accelerations
aA and aB are seen in the inertial reference frame, the termsFor constant angular acceleration,
a = 0, three terms remain on the right hand side; the centripetal acceleration Wx(WxrAB), the relative acceleration and the Coriolis acceleration.When acceleration relative to the rotation of the reference frame is accounted as in the example above the equations of moti0n in a rotating reference frame become:
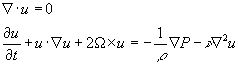
The Coriolis acceleration appears explicitly on the left hand side while the centripetal acceleration and the body force (assumed to be conservative) are combined with the pressure to form a reduced pressure
P.