Complex variables

Complex variables are very powerful in dealing with 2D irrotational incompressible flows.

Define:

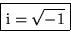
then cannot be found anywhere on the real axis. This allows us to ``pack'' two real numbers into one complex number, eg:

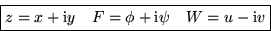
Here z is the complex position coordinate,

F is the complex velocity potential, and W is the complex conjugate (because of the - sign) velocity.

Complex numbers have the same general properties as ordinary numbers, except that they cannot be ordered (no >, <).

Exercise:

What are W and F for ideal stagnation point flow (u,v)= a(x,-y)? (Express in terms of z.)

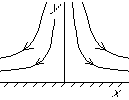
Homework: The exercise above.

03/09/01 0:01:42 03/09/01 0:10:49 03/19/01 0:01:11 03/19/01 0:22:46 03/19/01 0:23:24