- 01/07/03 W: Lecture.
- 01/09/03 F: Lecture.
- 01/12/03 M: Lecture.
- 01/14/03 W: Lecture.
[1.2, 1.3, 1.7 due.]
- 01/16/03 F: Lecture.
[2.1, 2.2, 2.5 due.]
- 01/19/03 M: Martin Luther King, Jr. day
- 01/21/03 W: Lecture.
- 01/23/03 F: Lecture.
- 01/26/03 M: Lecture.
[Due: 4.1,
1.1,
4.4 (functions T(x1,x2),b1(t),b2(t) are given),
4.2 (do not guess, use the appendices!),
4.7 (integrate around a circle around the origin in (c), but around
an arbitrarily shaped contour in (b))
(comment on the error in the Stokes' result in (b)),
4.9.
]
- 01/28/03 W: Lecture.
- 01/30/03 F: Lecture.
- 02/02/03 M: Lecture.
[5.11, 12, 14 due.
In question 5.11, d is much larger than D, not the other way around.
In question 5.14 (13), the pressure is 700 kPa at the nozzle entrance.
]
- 02/04/03 W: Lecture.
[5.16, 17 due
In 5.16, it can be assumed that no computer is available and that
the flow over the cone is quasi-steady relative to the cone.
In question 5.17, the book means that a part with diameter D/4
of the incoming stream enters the cone, while the remainder
between D/4 and D continues to pass around the outside of the cone.
]
- 02/06/03 F: Lecture.
- 02/09/03 M: Lecture.
[5.1, 5.3 due.]
- 02/11/03 W: Lecture.
- 02/13/03 F: Lecture.
- 02/16/03 M: Exam 1.
- 02/18/03 W: Lecture.
[Spherical finite volume due.]
- 02/20/03 F: Lecture.
[5.2 due.]
- 02/23/03 M: Lecture.
[5.6 and 5.8 due.
In question 5.6, take the curl of the differential momentum equation.
The book's Z is the height h. Also, assume that it is a Newtonian
fluid: there are no viscous stresses if a Newtonian fluid is at rest.
]
- 02/25/03 W: Lecture.
- 02/27/03 F: Lecture.
- 03/01/03 M: Lecture.
[6.3 and 6.5 due.
In 6.3, explain why this flow is not called inviscid but does
have an inviscid velocity field.
In 6.5, look up the incompressible continuity equation and momentum
equations in cylindrical coordinates (Appendix C, constant viscosity
and density,) substitute in the given velocities, (
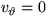 ),
verify that the continuity equation is already satisfied, and find
the single scalar pressure field that ensures that the three momentum
equations are also all satisfied. The pressure must of course be the
same pressure in all three equations.
]
),
verify that the continuity equation is already satisfied, and find
the single scalar pressure field that ensures that the three momentum
equations are also all satisfied. The pressure must of course be the
same pressure in all three equations.
]
- 03/03/03 W: Lecture.
- 03/05/03 F: Lecture.
- 03/08/03 M: Spring Break.
- 03/10/03 W: Spring Break.
- 03/12/03 F: Spring Break.
- 03/15/03 M: Lecture.
[Due: (A) Find the continuity equation and momentum equations in
cylindrical coordinates for an incompressible fluid when vr=vz=0
and neither velocity nor pressure depends on z. Work these
equations out as far as possible, finding the most precise
expression for the pressure and partial differential equation for
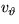 . (B) Now assume that the flow is steady. Also, assume that
that the streamlines are complete circles; this will allow you to say
something more about the integration constants of the pressure field,
since the pressure must return to the same value when
. (B) Now assume that the flow is steady. Also, assume that
that the streamlines are complete circles; this will allow you to say
something more about the integration constants of the pressure field,
since the pressure must return to the same value when 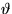 increases
by 2
increases
by 2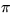 . Solve the resulting ordinary differential equation for
. Solve the resulting ordinary differential equation for
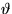 . (C) Put in the boundary condition that at r=Ri, the
fluid ends at a cylinder rotating with an angular speed
. (C) Put in the boundary condition that at r=Ri, the
fluid ends at a cylinder rotating with an angular speed 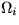 , giving the boundary condition
, giving the boundary condition 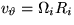 at r=Ri.
Also put in the boundary condition that at a larger r=Ro, the fluid
meets an outer rotating cylinder:
at r=Ri.
Also put in the boundary condition that at a larger r=Ro, the fluid
meets an outer rotating cylinder: 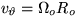 at r=Ro.
Use these boundary conditions to find the integration constants in the
expression for
at r=Ro.
Use these boundary conditions to find the integration constants in the
expression for 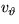 . (D) Identify the special flow fields
that arise when (a)
. (D) Identify the special flow fields
that arise when (a) 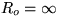 and
and 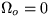 , and (b) Ri=0.
You can find these derivations in graduate fluid books like Curry's,
but try to do it from scratch.]
, and (b) Ri=0.
You can find these derivations in graduate fluid books like Curry's,
but try to do it from scratch.]
- 03/17/03 W: Lecture.
- 03/19/03 F: Lecture.
- 03/22/03 M: Exam II.
- 03/24/03 W: Lecture.
[18.8 due.
In 18.8, write the problem for either the streamfunction
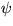 or
the potential
or
the potential 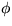 and solve using an appropriate method. The boundary
conditions are that (a) u=U0 + U(y) at x=0, 0 < y < h, (b) the flow
remains finite at
and solve using an appropriate method. The boundary
conditions are that (a) u=U0 + U(y) at x=0, 0 < y < h, (b) the flow
remains finite at 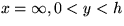 , and (c,d) the duct walls
, and (c,d) the duct walls
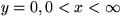 and
and 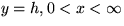 are streamlines (the vertical
velocity component is zero at walls.) Compare the properties of this
inviscid ``entrance'' flow with the viscous developed duct flow of
chapter 7.]
are streamlines (the vertical
velocity component is zero at walls.) Compare the properties of this
inviscid ``entrance'' flow with the viscous developed duct flow of
chapter 7.]
- 03/26/03 F: Lecture.
- 03/29/03 M: Lecture.
[18.1, 18.2, and the first part of 18.3 due.
In 18.3, use the trig addition formulae on page 44 of the math handbook
and the relationships with hyperbolic functions on page 58 to write
the sine in terms of real functions and i only.]
- 03/31/03 W: Lecture.
[Due:
- 1.
- Find the real and imaginary parts of: (1+i)2, (1+i)(1-i),
1/(1+i),
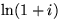 ,
,  . Plot the results in the
complex plane and find their magnitude and argument.
. Plot the results in the
complex plane and find their magnitude and argument.
- 2.
- For the following complex potentials, find the velocity
potential
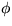 and the streamfunction
and the streamfunction 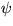 , and sketch the
streamlines: z, iz, z2,
, and sketch the
streamlines: z, iz, z2, 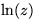 ,
, 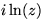 .
. - 3.
- For the same velocity potentials, find the complex conjugate
velocity W in terms of z, the Cartesian velocity components u
and v in terms of x and y, and the polar velocity components
ur and
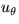 in terms of r and
in terms of r and 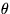 .
.
]
- 04/02/03 F: Lecture.
- 04/05/03 M: Lecture.
[18.6 due.]
- 04/07/03 W: Lecture.
- 04/09/03 F: Lecture.
[18.4, 18.5, 18.9 due.]
- 04/12/03 M: Lecture.
[18.7, 18.19 due. Also integrate the pressure distribution on the
surface of a cylinder with circulation in a cross flow to find
the force on the cylinder.]
- 04/14/03 W: Lecture.
[Due:
(1) Compute the Reynolds number of your car (based on driving
velocity and height, and of a plane of characteristic size 20 m
flying at Mach 0.8 in standard conditions.
(2) What is the flow velocity of water in a pipe of diameter 0.1 m if
the Reynolds number based on diameter and average velocity is 1.
(3) List other nondimensional numbers than the Reynolds number that
need to be the same for flows that look similar to be really
similar. Think of high-speed planes, ships, etcetera.
]
- 04/16/03 F: Lecture.
[Due:
(1) Identify the boundary layer coordinates and velocity components
for the boundary layer around a circular cylinder in terms of more usual
coordinates.
(2) For the same case, identify the boundary velocity ue just
above the boundary layer and the pressure pe just above the
boundary layer from the potential flow solution.
]
- 04/19/03 M: Lecture.
[Due:
(1) Using the results of the previous homework, formulate the
boundary layer problem for the impulsively started cylinder.
(2) Rewrite the Navier Stokes equations for the exact problem in
terms of the boundary layer variables and compare them to the
boundary layer approximation. What terms are lost in the boundary
layer approximation?
]
- 04/21/03 W: Lecture.
- 04/23/03 F: Lecture.
[Due:
(1) Find the shear force on a plate of length 0.5 m moving flush
through air at a speed of 0.5 m/sec
(2) Derive the steady boundary layer problem along a semi-infinite plate if
instead of a uniform flow, there is a sink sitting at the nose of
the plate. In other words, the potential flow just above the
boundary layer is 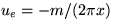 .
.
(3) Solve the previous boundary layer problem. The boundary layer
solution is again similar, but the boundary layer thickness is now
linear in x. In other words, u(x,y)=ue(x) f'(y/x),
where 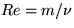 ]
]
- 04/27/03: Tuesday final 3:00-5:00 pm (ignore FSU schedule).
![]() . (B) Now assume that the flow is steady. Also, assume that
that the streamlines are complete circles; this will allow you to say
something more about the integration constants of the pressure field,
since the pressure must return to the same value when
. (B) Now assume that the flow is steady. Also, assume that
that the streamlines are complete circles; this will allow you to say
something more about the integration constants of the pressure field,
since the pressure must return to the same value when ![]() increases
by 2
increases
by 2![]() . Solve the resulting ordinary differential equation for
. Solve the resulting ordinary differential equation for
![]() . (C) Put in the boundary condition that at r=Ri, the
fluid ends at a cylinder rotating with an angular speed
. (C) Put in the boundary condition that at r=Ri, the
fluid ends at a cylinder rotating with an angular speed ![]() , giving the boundary condition
, giving the boundary condition ![]() at r=Ri.
Also put in the boundary condition that at a larger r=Ro, the fluid
meets an outer rotating cylinder:
at r=Ri.
Also put in the boundary condition that at a larger r=Ro, the fluid
meets an outer rotating cylinder: ![]() at r=Ro.
Use these boundary conditions to find the integration constants in the
expression for
at r=Ro.
Use these boundary conditions to find the integration constants in the
expression for ![]() . (D) Identify the special flow fields
that arise when (a)
. (D) Identify the special flow fields
that arise when (a) ![]() and
and ![]() , and (b) Ri=0.
You can find these derivations in graduate fluid books like Curry's,
but try to do it from scratch.]
, and (b) Ri=0.
You can find these derivations in graduate fluid books like Curry's,
but try to do it from scratch.]
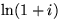 ,
,  . Plot the results in the
complex plane and find their magnitude and argument.
. Plot the results in the
complex plane and find their magnitude and argument.
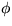 and the streamfunction
and the streamfunction 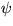 , and sketch the
streamlines: z, iz, z2,
, and sketch the
streamlines: z, iz, z2, 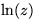 ,
, 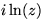 .
. 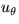 in terms of r and
in terms of r and 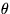 .
. ![]() .
.![]() ]
]