| Fall 2006 Homework Problems |
|
© Leon van Dommelen |
All problems are for incompressible flow (constant density and
coefficient of viscosity.)
- 7.9. You can assume that the film thickness is so small that
the curvature of the pipe wall can be ignored. In that case, it
becomes 2D steady flow along a flat wall of spanwise length
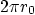 in the
in the 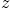 -direction. Steady 2D flow means in this case that
velocity and pressure are independent of
-direction. Steady 2D flow means in this case that
velocity and pressure are independent of 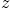 and time
and time 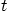 and that
the velocity in the
and that
the velocity in the 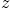 -direction
-direction 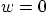 . Do not ignore gravity.
Assume ``developed flow'' in which the velocity components
have become independent of
. Do not ignore gravity.
Assume ``developed flow'' in which the velocity components
have become independent of 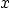 (taken to be downwards, with
(taken to be downwards, with 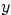 the distance from the cylinder surface). For the boundary
conditions at the free surface, assume that the liquid meets air
of zero density and constant pressure
the distance from the cylinder surface). For the boundary
conditions at the free surface, assume that the liquid meets air
of zero density and constant pressure 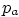 there. Also write
appropriate boundary conditions where the fluid meets the cylinder
surface. Do not make any other assumptions than listed above;
they should be all you need.
there. Also write
appropriate boundary conditions where the fluid meets the cylinder
surface. Do not make any other assumptions than listed above;
they should be all you need.
- What is the wall shear for the previous flow? Explain this
value physically.
- 7.5 Ignore gravity. To be original, assume that, in
cylindrical coordinates, the streamlines are circles around the
axis (which tells you that some velocity components are zero) and
that the velocity and pressure are steady and independent of the
axial coordinate
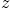 . Do not assume that the velocity
components are independent of
. Do not assume that the velocity
components are independent of 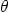 . Skip the
. Skip the  -momentum
equation for now, you can do without by showing that the pressure
gradient in the
-momentum
equation for now, you can do without by showing that the pressure
gradient in the 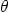 direction must be zero. To show that the
pressure gradient in the
direction must be zero. To show that the
pressure gradient in the 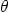 direction is zero, first show
that it must be independent of
direction is zero, first show
that it must be independent of 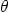 , (like we showed in class
for duct flow). Next integrate to find the form of the pressure
and use the fact that the pressure at a given point must have a
unique value, so that if
, (like we showed in class
for duct flow). Next integrate to find the form of the pressure
and use the fact that the pressure at a given point must have a
unique value, so that if 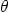 increases by
increases by 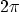 , the
pressure must return to the same value. (p 785 has the NS
equations you need and 781 the continuity equation.)
, the
pressure must return to the same value. (p 785 has the NS
equations you need and 781 the continuity equation.)
- Show that the skipped
 -momentum equation in the previous
problem can also be satisfied, and give the most general pressure
if all equations are satisfied.
-momentum equation in the previous
problem can also be satisfied, and give the most general pressure
if all equations are satisfied.
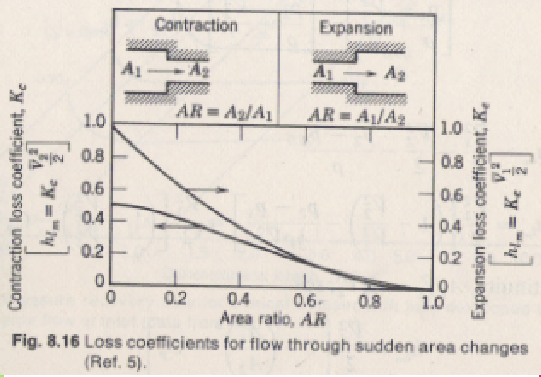
- (noncredit question) Consider the below graph for the minor
head losses due to sudden changes in pipe diameter:
Discuss the following issues as well as possible from the sort of flow
you would expect.
- How come the head loss become zero for an area ratio equal to 1?
- Why would the head loss be exactly one for a large expansion?
Coincidence?
- Why would the head loss be less than one if the expansion is
less? If the expansion is less, is not the pipe wall in the
expanded pipe closer to the flow, so should the friction with the
wall not be more??
- Why is there a head loss for a sudden contraction? The
mechanism cannot be the same as for the sudden expansion, surely?
Or can it?