| Fall 2007 Homework Problems |
|
© Leon van Dommelen |
This homework considers the flow around a flat plate airfoil and a
symmetric Joukowski airfoil using conformal mapping from the flow
around a cylinder.
The flow around the cylinder is described in a 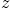 -plane by the
complex velocity potential:
-plane by the
complex velocity potential:
where
Take the radius of the cylinder to be
with value for  as specified below. Take
as specified below. Take 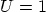 and
and
 for an incoming flow at an angle of attack of 20
degrees. The values of
for an incoming flow at an angle of attack of 20
degrees. The values of 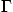 to use are specified below.
to use are specified below.
The airfoil plane is described in terms of a coordinate
which can be computed from 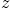 using the shifted Joukowski transform
using the shifted Joukowski transform
Use a software package like matlab that can handle complex numbers,
and create a polar coordinates mesh around the cylinder in the
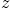 -plane. (Which will correspond to a nonpolar mesh in the
-plane. (Which will correspond to a nonpolar mesh in the
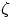 -plane.) In matlab,
-plane.) In matlab, real() will evaluate the real
part of a complex number and imag() the imaginary part.
- Taking
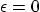 and
and 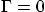 , evaluate the imaginary part
of
, evaluate the imaginary part
of 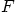 , giving the streamfunction
, giving the streamfunction 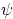 , and then use a contour
plotting package to plot the streamlines in the
, and then use a contour
plotting package to plot the streamlines in the 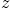 -plane. You may
need to first evaluate
-plane. You may
need to first evaluate 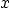 and
and 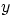 as the real and imaginary parts
of
as the real and imaginary parts
of 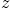 . Verify that the streamlines describe the circulationless
ideal flow around a cylinder.
. Verify that the streamlines describe the circulationless
ideal flow around a cylinder.
- Evaluate the pressure from Bernoulli, using the fact the
the derivative of
 gives the complex conjugate velocity, so
gives the complex conjugate velocity, so
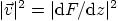 , (make sure to use the absolute
value function here, not just the square, since
, (make sure to use the absolute
value function here, not just the square, since 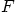 is complex).
Take the pressure zero at infinity. Plot isobars.
is complex).
Take the pressure zero at infinity. Plot isobars.
- Now evaluate the
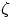 values, and then plot the streamlines
in the
values, and then plot the streamlines
in the 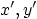 -plane. Verify that you get the flow around a flat
plate at an angle of attack, but that the Kutta condition is not satisfied.
-plane. Verify that you get the flow around a flat
plate at an angle of attack, but that the Kutta condition is not satisfied.
- Evaluate the circulation from the Kutta condition that
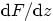 must be zero at the trailing edge
must be zero at the trailing edge 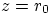 .
.
- Replot the streamlines in the
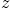 -plane.
-plane.
- Replot the streamlines in the
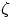 -plane.
-plane.
- Set
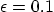 . Replot the streamlines in the
. Replot the streamlines in the 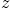 -plane.
-plane.
- Replot the streamlines in the
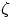 -plane.
-plane.
![]() -plane by the
complex velocity potential:
-plane by the
complex velocity potential:
![]() -plane. (Which will correspond to a nonpolar mesh in the
-plane. (Which will correspond to a nonpolar mesh in the
![]() -plane.) In matlab,
-plane.) In matlab,