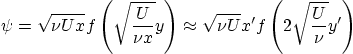15 12/07

1. Plot the wall shear in Blasius flow along a flat plate against $x$. Take the density, potential flow velocity and plate length to be one. Take the Reynolds numbers to be 100, 1,000, and 10,000 and restrict the x-values to plot $\tau_w$ on a scale from zero to one. In matlab, you would use the plot and maybe hold commands. Verify that the highest Reynold number has the lowest wall shear.

2. Plot the streamlines around the impulsively started circular cylinder. According to the Blasius two-term solution mentioned earlier, the streamfunction is given by:
   
   $$\psi= {\textstyle\frac12}u_e\left[r-\frac{r_0^2}{r}\right]... ...1\left(\frac{y}{\sqrt{4\nu t}}\right) \sqrt{4\nu t} - u_e y$$
   
   
   with $u_e=2U\sin\theta$ again the velocity just above the boundary layer. You should be able to recognize the first term as the potential flow streamfunction. The second term represents the approximation of the boundary layer flow as Stokes' second problem; $\zeta_0$ is the integral of the error function. The third term is the second order time term added by Blasius. The final $u_ey$ term is the ``matching'' part that the boundary layer solution and the potential flow have in common; it must be substracted in order to avoid having it double. Of course, $y$ is again the boundary layer coordinate.

   Function $\zeta_1$ can in principle be found by integrating function $\zeta_1'$ of the previous homework, but you saw what a mess that was. It is neater to simply integrate the system of ordinary differential equations satisfied by $\zeta_0$ and $\zeta_1$:
   

   $$\zeta_0''' + 2 \eta\zeta_0'' = 0 \qquad \zeta_1''' + 2 \eta\zeta_1'' - 4 \zeta_1' = 4 ({\zeta_0'}^2-\zeta_0\zeta_0''-1)$$
   
   
   This can be converted into a first order system, a matlab version of which you can find here. This can be integrated and the streamlines then plotted; this is done by the matlab program that you can find here.

   Run the program and verify that recirculatory streamlines occur at the rear of the cylinder, as a first step in creating the wake.

   Now copy the program to another name and remove the second order term of Blasius. Remove all traces, such as variables that are no longer used and update all comments. Replot, and comment on why the term added by Blasius is important for understanding the flow development.

   Now copy the program to another name and remove the first order, Stokes second problem, term too. Comment on the effect that this term has compared to the potential flow streamlines. (You can let this program inherit the $r$-values from the previous one, but add a comment near the start of the file that it needs to do so.)

3. Now copy the program to another name and modify it to plot the lines of constant vorticity according to the full Blasius expansion. Note that the potential flow term in the streamfunction expression above has no vorticity, and that the vorticity of the boundary layer terms can be approximated as $-\partial{u}/\partial{y}=-\partial^2\psi/\partial{y^2}$. The derivatives of the $\zeta$ functions can be found at various locations in the array zeta_vals returned by ode45. Since the vorticity values at high Reynolds numbers are large, you may want to plot from -110 to 110 in increments of 20. In particular, avoid plotting the zero vorticity line since it is extremely round-off sensitive. Comment on where the vorticity can and cannot be found in high-Reynolds number flow. According to the Stokes second problem approximation, the boundary layer thickness would be the same along the cylinder, take it $\sqrt{4\nu t}$. Is this still true when Blasius second term is included? If not, where is the boundary layer thicker? What would you think about what happens to the boundary thicknesses at the front and rear for large times (where the Blasius solution no longer applies?)

4. Program blaspsi.m found here plots the streamlines around a semi-infinite flat plate. Using the matlab hold and plot commands, add the displacement thickness curve $\delta^*$ to the graph in blue, and the rough total boundary layer thickness $\delta$ in red (for the latter, you may assume that the boundary layer vorticity is pretty much gone at $\eta=4$.) You can find the wall $x$-values $x>0,y=0$ somewhere in the two-dimensional mesh array x. Are the streamlines parallel to the plate with the displacement thickness added? If not, why not? To better see which streamlines are parallel to the thickened plate, also plot displacement curves shifted upwards by 0.025, 0.05, and 0.1, in green. Comment on in what sense the effect of the boundary layer is to thicken the plate by the displacement thickness.

   You may wonder about the use of ``optimal coordinates.'' The Blasius solution is written in terms of conformally mapped coordinates
   

   $$x'+iy' = \zeta = \sqrt{z} = \sqrt{x+iy}$$
   
   
   For a thin boundary layer, $y$ is small and then by approximation
   
   $$x' \approx \sqrt{x} \mbox{ and } y' \approx \frac{{\rm d}\zeta}{{\rm d}z} y = \frac{1}{2\sqrt{x}} y$$
   
   
   Using these approximations, the Blasius expression for the streamfunction is
   
   $$\psi = \sqrt{\nu U x} f\left(\sqrt{\frac{U}{\nu x}}y\right) \approx \sqrt{\nu U} x' f\left(2\sqrt{\frac{U}{\nu}}y'\right)$$
   
   
   Note that the final expression is perfectly regular, free of the artifacts caused by the factors $\sqrt{x}$ in the original Blasius expression. Not only that, it turns out that the final expression already contains the boundary layer displacement effect on the potential flow, without having to add that explicitly!

5. Read the descriptions in the book on how the steady flow field around a sphere and cylinder varies qualitatively with Reynolds number, from the bottom of page 323 on. Summarize it in about hundred words. (No more than 200.)

6. Look at Shankar Subramaniam's results of unsteady flow around a circular cylinder. Summarize it in about hundred words. (No more than 200.)

7. Look at Dr. Van Dommelen's results for unsteady flow around an airfoil. (Can you also see the ``starting vortex'' that comes off the trailing edge before the flow breaks away from the leading edge?) Summarize it in about hundred words. (No more than 200.)