| Example Project Description Question and Answers |
|
|
|
Example Project Description Question
Question:
Describe the project in which you plotted streamlines around an
airfoil using a complex velocity potential. Include
- Equations solved. Physical meaning of the equations.
- Boundary conditions, if any. Physical meaning of the boundary
conditions.
- Results obtained in the project. What these results mean
physically.
Ideal student answer
-
- Equations solved
- Physical meaning of the equations solved
- Viscous effects are ignored.
- The incoming air is free of vorticity.
- Flows around circles in the
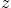 -plane are mapped to
airfoils in the
-plane are mapped to
airfoils in the 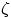 -plane.
-plane.
- Small constant
 is a measure of the thickness of
the airfoil. A flat plate airfoil is found for
is a measure of the thickness of
the airfoil. A flat plate airfoil is found for 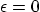 .
.
- The airfoils are called Joukowski airfoils.
- The Kutta condition prevents the potential flow going
around the traling edge of the airfoil.
- The Kutta condition ensures that the trailing edge point
is a stagnation point in the
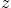 -plane.
-plane.
- Boundary layers will simply not go around a trailing edge.
-
- Boundary conditions, if any
- On the surface of the airfoil:
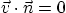 , the
airfoil is a streamline
, the
airfoil is a streamline 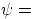 constant.
constant.
- At large distances, the horizontal component of the
air velocity is the constant
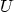 , and the vertical component
is
, and the vertical component
is 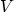 .
.
- Physical meaning of the boundary conditions
- There is no penetration of air into the surface of
the airfoil, nor motion away from it that would leave
a vacuum.
- However, the flow will slip along the surface, in violation
of the no-slip condition of viscous fluids.
- As a result, there are no boundary layers.
- The far-field boundary condition can be thought of as making
this the flow field of an airfoil moving through an atmosphere
otherwise at rest (but seen by an observer moving along with the
airfoil, not by one at rest compared to the far-field
atmosphere.
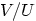 is the angle of attack, the angle between the chord
and the motion.
is the angle of attack, the angle between the chord
and the motion.
-
- Results obtained
- The flow around a reasonable airfoil shape was obtained.
- The airfoil trailing edge was a cusp, not a wedge.
- The airfoil was symmetric.
- When the circulation was not correct, the streamlines bend
around the trailing edge.
- When it was, the streamline left the trailing edge
tangentially.
- The effects of the airfoil on the streamlines die out quite
quickly with distance.
- The streamlines really bunch up near the leading edge.
- Physical meaning of the results
- Structurally, a Joukowski airfoil is not ideal.
- There must be a suction peak near the leading edge.