3 HW 3

In this class,

• Questions must be answered in order asked.
• Solutions must be neat.
• You must use the given symbols.
• You must show all reasoning.
• Copying is never allowed, even when working together.

1. For the Poisseuille flow of the previous homework, find the viscous stress tensor and the total stress tensor at an arbitrary radial position $r$ from the axis. Assume a Newtonian fluid. Show the stresses acting on a small volume ${\rm d}r{\rm d}\theta{\rm d}z$ at an arbitrary radius $r$ graphically in the $r,z$-plane. (Describe the stresses on its two surfaces normal to $\hat\imath _\theta$ only in words.) Include the pipe in the picture.

2. Repeat the previous question, but now do it in principal axes.

3. You may have noticed that if a stream of water exits a faucet, immediately after it exits, it contracts. The radius of the stream rapidly decreases. The stream is thinner below the faucet exit than the faucet exit. This effect has nothing to do with gravity, and everything with viscosity. Your task is to explain why this happens and find out by what factor the stream gets thinner under idealized conditions. Ignore gravity. Use a control volume that is a circular cylinder of finite length. Take one end of the cylinder to be the circular exit area of the faucet. That is your surface 1. The other circular end is surface 2. Since the stream gets thinner, the stream will only occupy the center part of surface 2. There is no mass flow through the outer ring. (The density of air is assumed zero, and its viscosity too, but it has a pressure.) Take the curved surface of the cylinder to be surface 3. Sketch the flowfield and control volume. Assuming that at surface 1, the velocity is our beloved axial Poiseuille flow
   
   $$\vec v = \hat\imath _z v_{\rm max} \left(1 -\frac{r^2}{R^2}\right)$$
   
   
   write the mass and momentum outflows $\int\rho\vec{v}\cdot\vec{n}{ \rm d}{A}$ and $\int\rho\vec{v}\cdot\vec{n}\vec{v}{ \rm d}{A}$ for this surface. (Recall that ${\rm d}{A}=r{\rm d}{r}{\rm d}{\theta}$ in polar coordinates in a plane of constant $z$.) Also write these integrals for surface 3. For surface 2, assume that at this position, viscous effects have smoothed out the initial parabolic velocity profile to a uniform one, in which all particles now move at the same velocity $V_{\rm e}$. As already noted the area $A_{\rm e}$ is less than the cross sectional area of the cylinder. At this time, $V_{\rm e}$ and $A_{\rm e}$ are still unknowns. Write the mass and momentum outflows through surface 2 in terms of these unknowns.

4. Continuing the previous question, write the $z$-components of surface force integrals for surfaces 1, 2, and 3. You can assume that $\tau^{\rm viscous}_{zz}$ is negligible on surfaces 1 and 2, but other viscous stresses like say $\tau^{\rm viscous}_{zr}$ are not negligible on surface 1. You can assume the pressure is atmospheric on surface 1. What do you think of surface 2? Show all reasoning.

5. If you now write the equations of mass conservation and momentum conservation for the control volume, you get two equations that you can use to find expressions for $V_{\rm e}$ and $A_{\rm e}$. Use the expression for $A_{\rm e}$ to find the contraction factor of the stream. Notes: For a real faucet, the stream is probably turbulent, and the velocity profile at the faucet exit would be flatter than parabolic. This should reduce the contraction, because there is less change in velocity needed to create the uniform velocity profile. And gravity will also thin the stream, but not just at the exit but also further down.

6. In a piping system, a stream of water enters an elbow with a pressure of 325 kPa and a velocity of 5 m/s. The entrance area has a diameter of 3 cm. The elbow bends the stream around over 120 degrees and the water then exits at the ambient pressure of 100 kPa through an area one fifth of the entrance area. Use mass and momentum conservation to find the force required to keep the elbow into place. Hints: You may want to include the elbow itself in the control volume. 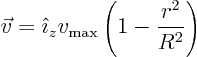(If you do not, do not forget to account for the pressure force that the atmospheric pressure exerts on the outer surface of the elbow.) Either way, you may want to use the concept of gauge,”or “gage, pressure to simplify the force integrals over the weird surfaces of your control volume. (See your undergraduate thermo or fluids book.)