8 HW 8

In this class,

• Questions must be answered in order asked.
• Solutions must be neat.
• You must use the given symbols.
• You must show all reasoning.
• Copying is never allowed, even when working together.

1. Find the expressions for $\hat\imath _r$, $\hat\imath _\theta$, and $\hat\imath _\phi$ in spherical coordinates in your notes. Now answer the following questions:
   1. What is the $x$-component of $\hat\imath _r$? What is the $z$-component of $\hat\imath _\theta$.
   2. Write the (vector) flow velocity $\vec v$ in terms of the spherical velocity components $v_r$, $v_\theta$, and $v_\phi$ and the unit vectors $\hat\imath _r$, $\hat\imath _\theta$, and $\hat\imath _\phi$. From that find the expression for the $x$-component of velocity $v_x$ in spherical coordinates. Do that by taking $x$-components of the vectors, not by making up nonexisting $x$-components of the scalars. Do the same for the $z$-component of velocity $v_z$. Finally, write the expression for the linear momentum in the $z$-direction in a volume of fluid in terms of the spherical coordinates $r$, $\theta$, and $\phi$ and spherical velocity components $v_r$, $v_\theta$, and $v_\phi$.
   3. Consider a spherical surface of radius $\ell$ around the origin. Find the unit vector $\vec n$ normal to that surface in terms of the spherical unit vectors $\hat\imath _r$, $\hat\imath _\theta$, and $\hat\imath _\phi$. Also find the spherical coordinates expression for the area ${\rm d}A$ of a little element ${\rm d}\theta{\rm d}\phi$ of this spherical surface. Find $\vec v\cdot\vec n$ in terms of $v_r$, $v_\theta$, and $v_\phi$. Find the $z$-component of $\vec v \cdot\vec n\vec v$ in terms of $v_r$, $v_\theta$, and $v_\phi$. Do that by taking $z$-components of vectors, not by making up nonexisting $z$-components of scalars.
   4. Continuing with the spherical surface, find the $z$-component of vector $\vec n$. Find the $z$-component of $-p\vec n$. Find the expression for the $z$-component of the integral $\int -p\vec n{\rm d}A$ over the spherical surface.
   5. Continuing with the spherical surface, in terms of the viscous stress tensor
      
      $$\bar{\bar\tau} = \left( \begin{array}{ccc} \tau_{rr} & \... ...r} & \tau_{\phi\theta} & \tau_{\phi\phi} \end{array} \right)$$
      
      
      find the force per unit spherical surface area $\bar{\bar \tau}^{\rm T}\vec n$ as a column of spherical stress components. Combine the components into an actual vector using $\hat\imath _r$, $\hat\imath _\theta$, and $\hat\imath _\phi$. Find the $z$-component of that vector. Find the expression for the $z$-component of the integral $\int \bar{\bar \tau}\vec n{\rm d}A$ over the spherical surface.
   6. Now reconsider the Stokes flow around a sphere done in a previous homework set, 6.6. Take as control volume the sphere $r\le\ell$ with as surface the spherical surface $r=\ell$. Write the integral $z$-momentum equation for this control volume. Ignore gravity. But besides the usual surface force integrals, you should also include the external force needed to prevent the sphere from being blown away. This external force is, of course, equal to the drag force $D$ that the fluid exerts on the sphere.
   7. Substitute in the Stokes flow velocity components and pressure and viscous stresses of the earlier homework. Assume that $\ell$ is much larger than the radius of the sphere $R$, so that you can ignore the $O(1/\ell^4)$ terms in the viscous stresses. If the stresses in your earlier homework solution were not correct, get the correct ones from the posted homework.
   8. Do the integrals and take the limit that $R/\ell\to0$. Do you get the correct drag force of the sphere?

2. In an earlier homework set, 7.1, you solved a viscous flow around a rotating axis. This flow has circular streamlines. For this viscous flow, how much of the centripetal acceleration of the fluid particles comes from the pressure force per unit volume and how much from the viscous force per unit volume?

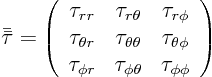
3. In an earlier homework set, 5.2, you examined ideal stagnation point flow. Have another look at that solution (the correct solution is on the web). Was the pressure given by the Bernoulli law, even though the flow was assumed to be viscous? So, was the viscous stress zero? What was it? Was the viscous force per unit volume zero? The same things happen for any incompressible flow that is irrotational, i.e. for which the vorticity is zero. Such flows are also called ideal flows or potential flows. Now consider another irrotational flow that you looked at in an earlier homework, 4.6. This flow was unsteady. Was the viscous stress tensor zero? What was it? Was the viscous force per unit area zero? If so, then apparently the pressure was given by an extended Bernoulli law that applies to unsteady flow.

4. Derive the major head loss and friction factor for laminar pipe flow. Explain all reasoning. The solution for the pressure distribution in pipe flow can be found in almost any fluids book. Sketch a Moody diagram to show how the friction changes when the flow in the pipe becomes turbulent.

5. Consider the below graph for the minor head losses due to sudden changes in pipe diameter:
   
   Discuss the following issues as well as possible from the sort of flow you would expect.
   1. How come the head loss becomes zero for an area ratio equal to 1? Does that not violate thermodynamics? There is always some viscous friction, surely?
   2. Why would the head loss be exactly one for a large expansion? Coincidence?
   3. Why would the head loss be less than one if the expansion is less? If the expansion is less, is not the pipe wall in the expanded pipe closer to the flow, so should the friction with the wall not be more??
   4. Why is there a head loss for a sudden contraction? The mechanism cannot be the same as for the sudden expansion, surely? Or can it?