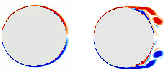
(Book 16.4)
At high Reynold numbers, vorticity is generated by solid surfaces in thin boundary layers. As long as these boundary layers do not separate from the walls, most of the flow field is not much affected by this vorticity.


We can describe the flow outside the regions containing vorticity using potential flow theory. We can describe the flow in the thin vorticity layers next to the surface using boundary-layer theory.
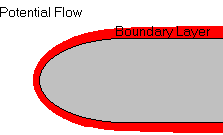
Boundary layer theory requires high Reynolds numbers. You need very different approximations for low Reynolds numbers.
Exercise:
Graphically compare the vorticity fields of the Stokes flow around a sphere (problem 6.1 in the book), valid for small Reynolds with that around an impulsively started circular for large Reynolds number. To get the velocity in the boundary layers of the impulsively started cylinder, assume that if we zoom in on a small piece of the surface of the cylinder, the flow looks like a Stokes' 2nd problem layer, (as seen in a coordinate system in which the plate is at rest and under an angle.)