Flat Plate

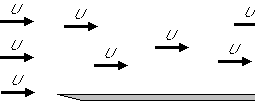
(Book 20.1)

We want to derive the Blasius steady boundary layer on a semi-infinite flat plate:

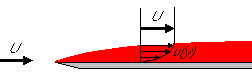
Continuity:

x-Momentum:

Note that since the velocity is constant, U, in the matching region, the pressure must be constant.

Try a similarity solution. If is a typical boundary layer thickness:

Typical boundary layer thickness:

Shape of the velocity profile: with

Numerical solution produces f''(0)=0.33206, which fixes the wall shear.

Exercise:

Find the shear force on a plate of length 0.5 m moving flush through air at a speed of 0.5 m/sec

Exercise:

Derive the steady boundary layer along a semi-infinite plate if instead of a uniform flow, there is a sink sitting at the nose of the plate. In other words, the potential flow just above the boundary layer is . The boundary layer solution is again similar, but the boundary layer thickness is now linear in x. In other words, u(x,y)=u_e(x) f'(y/x).