Developed

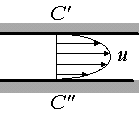
At and beyond station C the flow is called developed. We will assume that the flow is nonturbulent and that the streamlines have become parallel. These assumptions allow us to solve the incompressible Navier-Stokes equations exactly!

Note that for parallel streamlines, (unidirectional flow), v=0.

Continuity:

y-momentum:

x-momentum:

hence:

Exercise:

Why is it constant? If the duct is long, how can you approximate the constant? What is the sign of ?

The boundary conditions u(0)=u(h)=0 give the constants:

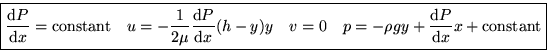
Maximum velocity:

Mass flux (per unit span):

The volumetric flow rate

Average velocity:

Note that and .

Vorticity:

Shear:

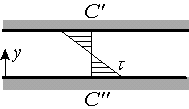
Exercise:

Verify the integral momentum equation for any duct length L.

• What is the rate of change of linear momentum inside?
• What is the net outflow of momentum through the boundary?
• What are the forces on the control volume?

Note that this flow becomes turbulent at a Reynolds number of say 1,500 (in the range from 1,000 to 8,000). The above expressions do not apply to turbulent flow.

You should now be able to do 7.1, 2, and 5 to 11 Notes:

• In 7.5, write and solve the Navier-Stokes equations in cylindrical coordinates assuming that
• In 7.9, write and solve the Navier-Stokes equations in cylindrical coordinates assuming that
• In 7.11, write and solve the Navier-Stokes equations in 2D planar flow for each fluid separately assuming that and . Carefully consider the boundary condition where the fluids meet.