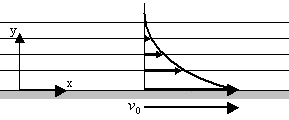
Stokes' first problem, also erroneously called Rayleigh flow:

Continuity:
![]()
y-momentum:
![]()
x-momentum:
![]()
The x-momentum equation becomes:
![]()
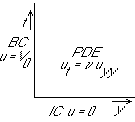
Exercise:
How would you normally find u?
A simpler way to solve is to guess that the solution is similar: after rescaling u and y, all velocity profiles look the same.
Original profiles:
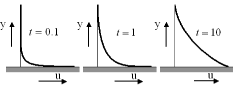
Supposed shape after scaling u with V0, and y with a
characteristic boundary layer thickness ![]() that increases
with time:
that increases
with time:
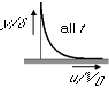
Mathematical form of the similarity assumption:
![]()
![]()
![]()
![]()
Solving the O.D.E.s for ![]() and f, we solve the P.D.E.
For the boundary layer thickness
and f, we solve the P.D.E.
For the boundary layer thickness ![]() so
so
![]()
For the velocity profile ![]() hence
hence
![]()
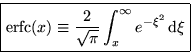
Exercise:
Derive the expressions forand f.
Total:
![]()
You should now be able to do 7.14, 16, 17