Decomposition

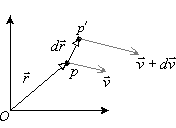
While the motion of individual points of fluid tells us things like the force on the fluid at that point, in order to understand effects such as viscosity we must look at deformation of the fluid. The local deformation of the fluid near some point P depends on how arbitrary neigboring points P' move compared to P. If all neighboring points P' move with the same velocity as P, the fluid moves as a solid block, and there is no deformation.

The motion of point P' relative to neighboring point P is given by the difference in velocity .

So the velocity derivative tensor A determines the rate of local deformation of the fluid.

To understand this better, take A apart into symmetric and antisymmetric parts:

The symmetric part is called the strain-rate tensor.

By rotating the coordinate system, to x',y',z', it becomes diagonal:

This are three simple straining motions.

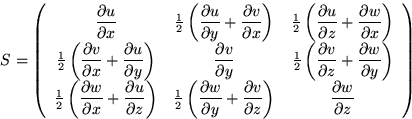
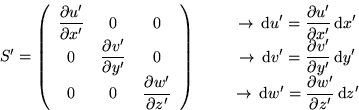
The trace of the tensor S is the rate of (relative volume) expansion of the fluid.

The second, antisymmetric, part of A looks as:

where

is the vorticity. By simply writing it out, you can see that the velocity due to this antisymmetric part is .That is the equation of a solid body rotation with an angular velocity vector equal to .

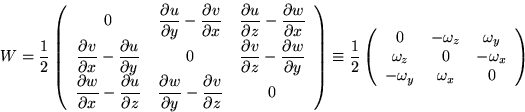
Vorticity is important because it allows flows to behave in complicated, nonlinear ways.

The line integral of the velocity along a closed contour is called the circulation of that contour:

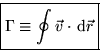
Exercise:

What can you say about if ?