Sometimes, writing the conservation laws for fixed volumes is not enough. For example, an emptying balloon is not a fixed volume. Nor is the human heart, an accelerating rocket, etcetera. But they are not material regions either. They are arbitrary regions (or control volumes).
Fortunately it is not difficult to go from the equation for a fixed
volume to one for a moving volume. Simply use the Leibnitz also on
the moving region, the same way we used it on the material region.
(Do not forget that the velocity of the boundary ![]() of the
moving region is not the same as the fluid velocity
of the
moving region is not the same as the fluid velocity ![]() on that
boundary.) We will skip the derivation.
on that
boundary.) We will skip the derivation.
The only point to remember is: if the boundary of the region
you are considering moves with speed ![]() , you need to replace
the
, you need to replace
the ![]() in the outflow correction integrals
with
in the outflow correction integrals
with ![]() . And it is not
difficult to see why: if the boundary moves with the same speed
as the fluid at that boundary, no fluid goes in or out!
. And it is not
difficult to see why: if the boundary moves with the same speed
as the fluid at that boundary, no fluid goes in or out!
So mass conservation for an arbitrary control volume is:
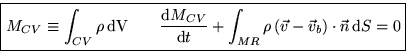 |
(27) |
Similarly the momentum equation becomes:
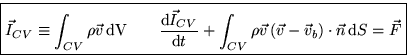 |
(28) |
Often, it is more convenient to use a moving coordinate system, say a coordinate system fixed to the accelerating rocket instead of to the ground. Trick two to remember is that you can get a momentum equation involving velocities relative to the moving coordinate system, (instead of absolute velocities), by substracting the continuity equation times the coordinate system velocity from the momentum equation above.
Example:
Problem: Write the equation of motion of a balloon in terms of the exit area and the relative exit velocity of the air from the balloon.
Solution: The control volume is the balloon. This is an arbitrary region.
Mass conservation:
The final integral over the rubber is zero (air velocity
and rubber velocity
are equal at the balloon surface.) The integral over the exit we will call
, so
Assuming that the relative air velocity at the exit is normal to it and constant:
Now the momentum equation. It reads
We write the linear momentum as
, in which
is an average velocity of the balloon and the air inside. Also, the integral over the rubber is again zero, and assuming that at the exit the air velocity
is about constant across the exit:
Substract
times the continuity equation:
Ignoring the difference between average velocity and the boundary velocity of the exit, the difference in velocities is just the relative velocity of the air at the exit. Also, we will assume one-dimensional motion and identify the force as being minus the drag force. So we finally get:
where D is the drag force and
the thrust force due to outflow. This can be solved along with
You should now be able to do questions 5.15, 5.16, 5.17.