Conformal Mappings

(Book 18.10)

Conformal transformations are a way to generate more complex flow fields from simple ones. They are based on distorting the independent variable: Suppose we are given a complex velocity potential F(z) depending on the complex coordinate z. Now let be another complex coordinate, then is also a complex velocity potential, provided only that is a differentiable function of z.

Reason: according to the chain rule, the derivative of exists and is equal to:

As an example of a conformal transformation, we will find the complex potential around a flat plate airfoil, an airfoil of vanishing thickness. We start with a flow field in a plane that is simply a cylinder of unit radius with (clockwise) circulation in a uniform stream U:

We are now going to deform this cylinder into a flat plate airfoil.

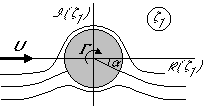
According to the Kutta condition, the rear stagnation point must be located at what will become the trailing edge of the airfoil. If the stagnation point is anywhere else, the flow must bend around the trailing edge:

Viscous effects do not allow that. So we must make sure that the rear stagnation point deforms into the trailing edge. To make this easier, we will first rotate the flow so that the rear stagnation point moves to the point 1:

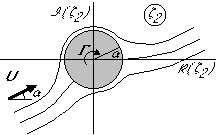
We can rotate the independent coordinate counter-clockwise like this by multiplying with a complex exponential:

where is the angular position of the rear stagnation point.

The potential is in terms of :

(The constant arising from the logarithm is of no importance.)

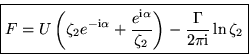
Finally, we ``squeeze the airfoil flat in the vertical direction'' to a plate:

The transformation that does this is the Joukowski transformation:

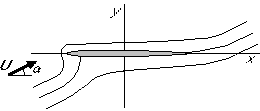
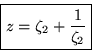
Exercise:

Show that the unit circle in the -plane, corresponds to a flat plate on the x-axis in the z-plane.

Note that the rear stagnation point becomes z=2, while becomes z=-2. As a result, the chord of the created airfoil is c=4.

Since for large distances, , the potential at large distances is

which is a uniform flow at an angle alpha with the x-axis (the chord of the airfoil.) This angle between the chord and the direction of the incoming stream is called the angle of attack of the airfoil.

The lift generated by the airfoil, will be normal to the free stream U. This lift will depend on the angle of attack: the lift is zero by symmetry when .

We now want to derive the relationship between the angle of attack and the lift. Remember that in the -plane, the angle determines the location of the rear stagnation point:

Writing in polar coordinates as , we get

Dividing by and solving for :

The lift of an airfoil is expressed in terms of a lift coefficient:

This formula is good approximation for the lift of thin airfoils in general. However, for airfoils that are not symmetric top/bottom, the angle should be measured from the direction of zero lift, instead of from the chord.

Exercise:

Find the velocity on top and bottom of the flat plate airfoil as a function of x.

Exercise:

Integrate this velocity to find the circulation around the airfoil. Is it equal to ?

Exercise:

Integrate the pressure difference over the airfoil to find the net force on it.

Exercise:

Is the result of the previous exercise as you expected? If not, what do you think is the difficulty?

Exercise:

Integrate the pressure difference over the the airfoil to find the moment around the center. From it , show that the resultant force acts at the point one-quarter chord behind the leading edge.

You should now be able to do The exercises above, 18.10, 11