Channel Flow

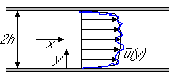
Assume that the flow is independent of x.

Continuity

Stress Tensor:

x Momentum:

y-Momentum:

From y-momentum:

where p_w is the pressure on the wall.

Put in x-momentum (with independent of x):

So, the total stress is linear in y, and vanishes (by symmetry) on the center line.

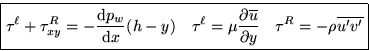
Since the Reynolds number is high (i.e. small) the laminar shear stress must be small over most of the cross section. However, the dissipation is not so small, and the loss of energy must come from the pressure gradient. Hence the pressure gradient required is much larger than for laminar flow. To balance, the Reynolds stress must be much larger than the stress in laminar duct flow.

However, at the wall, the Reynolds stress is zero because of no slip. So at the wall and close to it, the laminar shear stress must be large, which is only possible if is very large. But, since the profile is monotonuous to the center, this can only be true in a thin sublayer at the wall. Outside that layer, the Reynolds stress must dominate.

Exercise:

Sketch the velocity profiles for laminar and turbulent flow with the same mass flow through the duct. Indicate the layer near the wall and how it is different from the laminar flow case.

The magnitude of the shear stress at the wall is written in terms of a ``friction velocity'' u^*:

In the surface layer, we have the ``law of the wall'':

The bottom part of the surface layer is called viscous sublayer since the effective Reynolds number becomes too low for turbulence to sustain itself.

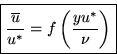
In the core region:

``Velocity defect law'':

The matching region is called inertial sublayer. In this layer, both results must be valid. In particular, if we match gradients,

which requires:

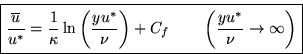
Substracting, we get the ``logarithmic friction law'':

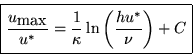
Exercise:

Discuss figure 23.13 and how it verifies and does not verify the above discussion for the case of a boundary layer.