12 11/27 M

1. Find the streamfunction for ideal flow around a circular cylinder where the incoming flow at large distances has velocity $\vec{v}=U{\widehat \imath}$ with $U$ a constant. To do so, first verify that $r^{\pm n}\cos(n\theta))$ and $r^{\pm n}\sin(n\theta))$ are solutions of the Laplace equation by plugging them into the Laplacian in polar coordinates. Next find the streamfunction that describes the $U{\widehat \imath}$ flow at large distances in Cartesian coordinates, and convert it to polar coordinates. Next add a multiple of a $r^{-n}\cos(n\theta))$ or $r^{-n}\sin(n\theta))$ term (with $n>0$ so that the flow at large $r$ is not affected) to satisfy the appropriate boundary condition at the cylinder surface $r=a$.

2. You should have found the streamfunction to be
   
   $$\psi = U \sin(\theta)\left(r-\frac{a^2}{r}\right)$$
   
   
   Find the polar velocity components on the surface of the cylinder from this streamfunction. (Note that appendix D.2 has an error; the correct equation is $v_\theta=-\partial\psi/\partial{}r$.) Is the velocity normal to the surface zero as it should be? Is the velocity tangential to the surface the same as we got from the velocity potential? Use the Bernoulli law to find the pressure on the surface in terms of the pressure $p_\infty$ far upstream. Where is the pressure on the surface $p_\infty$? Where do you have stagnation pressure on the surface?

3. The streamfunction of an ideal vortex at the origin equals $(\Gamma/2\pi)\ln r$. Show that this produces $v_r=0$ and $v_\theta=-\Gamma/2\pi r$. Add this to the streamfunction of the cylinder, above. Show that the velocity component normal to the surface is still zero. So we now have a cylinder with circulation around it. Recompute the pressure on the surface. Then integrate the pressure forces on the surface to find the net horizontal and vertical forces on the cylinder. According to D'Alembert, you should find that the horizontal force (the drag) is zero in this ideal flow. Is it? According to Kutta-Joukowski, you should find that the vertical force (the lift) is $\rho{}U\Gamma$. Is it?

4. Videos Dynamics: Potential flows: 290-294 and 299. In 290-293, do not try to accurately reproduce the body sizes. Just take the absolute values of the singularity strengths 2. And in 292, space them 4 intervals apart. In 294, just show the streamlines of the target flow, and comment on why one singularity is weird. In 299, try to match the experimental flow reasonably well. Note in doing so that you can put new singularities on top of old ones to adjust their strength; you do not have to start again from scratch. Alt-PrintScreen should send the plots to the clipboard, so that you can paste it into a program like MS Paint, where you can save it and print it out. 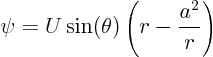In all cases, shade or highlight the part of the flow field that you would want to solidify (replace by a solid body like a cylinder or whatever). To get the body contour accurately, starting streamlines from near the stagnation points can be effective.

5. Go to the class airfoil programs page. Download Matlab program cylinder.m. Print it out and in the print-out mark where the complex potential for flow around a circular cylinder is being set. Also mark where the streamlines are being drawn, and how that works. Run the program in Matlab and print out the streamlines around a circular cylinder. Then set variable $\Gamma$ (Gamma) to an interesting value and print out those streamlines too.

6. Also download Matlab program airfoil.m. Mark where a cylinder potential is set in a complex $\zeta$-plane. Also mark where this cylinder is mapped to a Joukowski airfoil in a complex $z$-plane, and list the formula used to get $z$ from $\zeta$ that achieves this mapping. You may observe that program airfoil.m is astonishingly simple for the complexity of the flow and graphics that it produces.

   Then in Matlab, select parameters that produce the flow around a slightly cambered Joukowski airfoil of roughly 10% thickness ratio at 15 degrees angle of attack. List your parameters. Plot out the picture of the streamlines and isobars. Next set the circulation to zero by setting variables Gamma and auto both to zero and replot to show the effect of not satisfying the Kutta condition. Do the streamlines still come off smoothly from the trailing edge? What happens to the pressure?