6 10/18 W

1. 5.14. Find both the horizontal and vertical components of the force. Make sure that you clearly define what control volume you are using, as there is no unique choice.

2. 5.11. Cearly define what control volume you are using.

3. 5.12. This question explains why the water stream coming out of a faucet contracts in area immediately below the faucet exit. As always, both mass and momentum conservation are needed.

   The faucet exit velocity may be assumed to be of the form of Poisseuille flow:
   

   $$v_z = v_{\rm max} \left(1 - \frac{r^2}{R^2}\right)$$
   
   
   You can assume that the stress tensor at the faucet exit is of the form (in cylindrical coordinates)
   
   $$\bar{\bar\tau} = \left( \begin{array}{ccc} 0 & 0 & \tau_0 r/R 0 & 0 & 0 \tau_0 r/R & 0 & 0 \end{array} \right)$$
   
   
   in other words, much like the strain rate tensor that you derived earlier for Poisseuille flow.

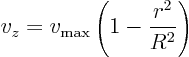
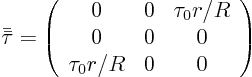
   Take the faucet exit as the entrance of your control volume. Take as exit to your control volume a slighly lower plane at which the radius of the jet has stabilized to $R_2$ and the flow velocity has become uniform (independent of r). For a uniform flow velocity there are no viscous stresses. Gravity can be ignored compared to the high viscous forces in this very viscous fluid. (However, over a longer distance gravity will lead to a further thinning of the jet.) And you can assume that the pressure at the exit is already atmospheric, as it definitely is in the lower plane below.