(Part of 7.17 with 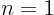 only.) Find the solution for the
velocity profile from the equation found in the previous question.
One way to do so is differentiate the equation for
only.) Find the solution for the
velocity profile from the equation found in the previous question.
One way to do so is differentiate the equation for 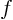 twice with
respect to
twice with
respect to 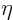 , and so show that
, and so show that 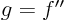 satisfies the equation
satisfies the equation
This equation is the same as the one for 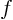 in Stokes’ second
problem, and was solved in class. The general solution was
in Stokes’ second
problem, and was solved in class. The general solution was
Explain why 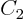 must be zero. Explain why then
must be zero. Explain why then 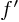 can be found as
can be found as
Draw the region of integration in the 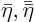 -plane.
Use the picture to change the order of integration in the multiple
integral and integrate
-plane.
Use the picture to change the order of integration in the multiple
integral and integrate 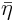 out. Show that
out. Show that
Integrate once more to find 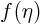 . Apply the boundary condition
to find
. Apply the boundary condition
to find 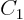 .
.
Another way to solve is find the solution in a suitable math
handbook. Note from the above that the solution is related to the
error function somehow. Unfortunately, basic handbooks may not have
the solution. You may need something more advanced.
![\begin{displaymath}
f'(\eta)= C_1
\left[
\eta\int_{\bar{\bar\eta}=\eta}^{\inf...
...ta}^2}
{ \rm d}\bar{\bar\eta} -\frac12 e^{-\eta^2}
\right]
\end{displaymath}](img118.gif)