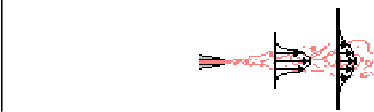
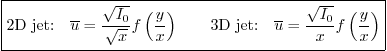Now consider a turbulent jet, as shown above. Here you would expect
that downstream
Again, 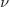 can be ignored, assuming that the turbulent Reynolds
number is large enough.
can be ignored, assuming that the turbulent Reynolds
number is large enough.
Also, it can again be assumed that the details of the initial
conditions become invisible sufficiently far downstream, with one
exception. Integral momentum conservation between any two downstream
positions of constant  implies that the
implies that the  -momentum flow integral
-momentum flow integral
must be the same at the two stations. (Pressure differences between
stations sufficiently far downstream can be ignored). So the momentum
flow integral above is a constant. It is determined by the strength
of the jet that the initial conditions generated. Since it is
constant, it cannot become invisible. Note that in the
incompressible case, you can more simply assume that
is constant. Also note that 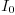 has units
has units 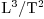 for a two
dimensional jet, where
for a two
dimensional jet, where 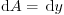 , but units
, but units 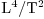 for a
three-dimensional jet, for which
for a
three-dimensional jet, for which 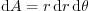 .
.
So the functional dependence can be simplified to
and dimensional analysis then produces
Cleaning this up gives:
Like for the mixing layer, the mean velocity profiles are similar, and
the jet thickness is proportional to  . But in the two-dimensional
case, the maximum jet velocity decays proportional to
. But in the two-dimensional
case, the maximum jet velocity decays proportional to 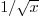 ,
slower than the
,
slower than the 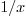 of the three-dimensional case.
of the three-dimensional case.
![]() implies that the
implies that the ![]() -momentum flow integral
-momentum flow integral