11 11/13 W

1. Find the streamfunction for ideal flow around a circular cylinder where the incoming flow at large distances has velocity $\vec{v}=U{\widehat \imath}$ with $U$ a constant. To do so, first verify that $r^{\pm n}\cos(n\theta))$ and $r^{\pm n}\sin(n\theta))$ are solutions of the Laplace equation by plugging them into the Laplacian in polar coordinates. Next find the streamfunction that describes the $U{\widehat \imath}$ flow at large distances in Cartesian coordinates, and convert it to polar coordinates. Next add a multiple of a $r^{-n}\cos(n\theta))$ or $r^{-n}\sin(n\theta))$ term (with $n>0$ so that the flow at large $r$ is not affected) to satisfy the appropriate boundary condition at the cylinder surface $r=a$.

2. You should have found the streamfunction to be
   
   $$\psi = U \sin(\theta)\left(r-\frac{a^2}{r}\right)$$
   
   
   Find the polar velocity components on the surface of the cylinder from this streamfunction. (Note that appendix D.2 has an error; the correct equation is $v_\theta=-\partial\psi/\partial{}r$.) Is the velocity normal to the surface zero as it should be? Is the velocity tangential to the surface the same as we got from the velocity potential? Use the Bernoulli law to find the pressure on the surface in terms of the pressure $p_\infty$ far upstream. Where is the pressure on the surface $p_\infty$? Where do you have stagnation pressure on the surface?

3. The streamfunction of an ideal vortex at the origin equals $(\Gamma/2\pi)\ln r$. Show that this produces $v_r=0$ and $v_\theta=-\Gamma/2\pi r$. Add this to the streamfunction of the cylinder, above. Show that the velocity component normal to the surface is still zero. So we now have a cylinder with circulation around it. Recompute the pressure on the surface. Then integrate the pressure forces on the surface to find the net horizontal and vertical forces on the cylinder. According to D'Alembert, you should find that the horizontal force (the drag) is zero in this ideal flow. Is it? According to Kutta-Joukowski, you should find that the vertical force (the lift) is $\rho{}U\Gamma$. Is it?

4. Consider a wall that for $x>0$ is along the $x$-axis. A fluid is flowing in the minus $x$-direction along this wall. At the origin however, the wall bends upwards by 30 degrees, producing an inside corner of 150 degrees. Find the expression for the complex velocity potential of this flow. To find the sign of the constant, find the velocity at a single, easy point, and check its sign. As noted, the flow must be going in the negative $x$-direction. Find the streamfunction and from that, sketch the streamlines. Find the velocity, and so show that the corner point is a stagnation point. Find the wall pressure and sketch its distribution with $x$.

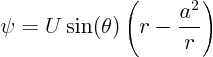
   In a real viscous flow at high Reynolds number, a thin boundary layer along the wall upstream of the corner will be unable to withstand much of the adverse pressure gradient slowing it down. So the boundary layer will separate before it reaches the corner, and reattach to the wall downstream of it. Based on that, sketch how you think the viscous streamlines will look like.

   Next assume that at the origin the wall bends downwards by 30 degrees, producing a 210 degree corner. Repeat the analysis and sketching. In this case you should find that there is infinitely large negative pressure at the corner. The boundary layer approaching the corner now finds things plain sailing until it reaches the corner. But right at the corner it is not going to go around it, as that would produce a very strong adverse pressure gradient. Instead the boundary layer just keeps going straight along the $x$-axis immediately behind the corner. That effectively eliminates the corner and its associated pressure gradient. This effect is why flows around airfoils with sharp trailing edges and sufficiently blunted leading edges satisfy the Kutta-Joukowski condition.

   Finally, if the flow is unsteady (i.e. if the constant in your complex potential varies with time), how does that affect whether the ideal flow at the corner has stagnation or infinitely negative pressure?

5. Videos Dynamics: Potential flows: 290-294 and 299. In 290-293, do not try to accurately reproduce the body sizes. Just take the absolute values of the singularity strengths 2. And in 292, space them 4 intervals apart. In 294, just show the streamlines of the target flow, and comment on why one singularity is weird. In 299, try to match the experimental flow reasonably well. Note in doing so that you can put new singularities on top of old ones to adjust their strength; you do not have to start again from scratch. Alt-PrintScreen should send the plots to the clipboard, so that you can paste it into a program like MS Paint, where you can save it and print it out. In all cases, shade or highlight the part of the flow field that you would want to solidify (replace by a solid body like a cylinder or whatever). To get the body contour accurately, starting streamlines from near the stagnation points can be effective.

6. Go to the class airfoil programs page. Download Matlab program cylinder.m. Print it out and in the print-out mark where the complex potential for flow around a circular cylinder is being set. Also mark where the streamlines are being drawn, and how that works. Run the program in Matlab and print out the streamlines around a circular cylinder. Then set variable $\Gamma$ (Gamma) to an interesting value and print out those streamlines too.