- If the density of air at sea level is 1.225 kg/m
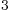 , and the
molecular mass 28 g/mol, then what is the number of molecules per
unit volume? What is the average spacing
, and the
molecular mass 28 g/mol, then what is the number of molecules per
unit volume? What is the average spacing 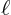 of the molecules?
(First compute the average volume per molecule, then think of the
molecules as being equally spaced in all three directions of a
of the molecules?
(First compute the average volume per molecule, then think of the
molecules as being equally spaced in all three directions of a
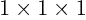 m
m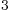 box)
box)
Consider a molecule of average diameter 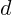 that moves over one free
path length
that moves over one free
path length 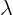 . During that motion it will hit another
molecule if the center of the other molecule is within a radius
. During that motion it will hit another
molecule if the center of the other molecule is within a radius 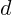 from the path of the molecule. In other words, the center of the
other molecule must be inside a cylinder of radius
from the path of the molecule. In other words, the center of the
other molecule must be inside a cylinder of radius 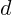 around the
path
around the
path 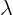 of the first molecule. There should be about one
collision in a free path, so there should be about one other
molecule within the cylinder. So the free path can be ballparked
from setting the volume of the cylinder equal to the average volume
per particle:
of the first molecule. There should be about one
collision in a free path, so there should be about one other
molecule within the cylinder. So the free path can be ballparked
from setting the volume of the cylinder equal to the average volume
per particle:
Take the average diameter of the molecules to be 0.3 nm and compute
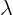 . A more careful analysis says you still need to divide
this by
. A more careful analysis says you still need to divide
this by 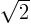 , so do so.
, so do so.
- Continuing the previous question, suppose you have a body of
typical size
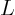 in the flow of some gas. Which length,
in the flow of some gas. Which length, 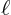 or
or
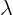 , relative to
, relative to 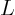 , determines whether you can define a
meaningful
, determines whether you can define a
meaningful pointwise
density and velocity at a given
time and position (by taking a small volume around the point and
then taking the ratio of mass inside to volume, respectively
momentum inside divided by mass inside at a given time)? (Of
course, the small volume must be small compared to the body for it
to be considered a point
instead of a region in the
flow.)
Which length determines whether you can define a meaningful
pointwise
density and velocity that would be enough
info, say, to compute the further flow development? In other words,
the pointwise density and velocity (and temperature) must fully
determine the state of the gas at the points.
In particular, take sea-level air like in the previous question.
Then for what body size 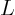 can you no longer use the normal
(Navier-Stokes) equations to compute the flow at the
can you no longer use the normal
(Navier-Stokes) equations to compute the flow at the
points
around the body? For what size body can you
no longer find a meaningful continuum velocity for the
points
around the body by averaging mass and
momentum in small volumes even if you used molecular dynamics?
- The Lagrangian equation for inviscid flow is Newton's second law
in the form
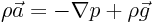 , i.e. mass per
unit volume times acceleration equals pressure force per unit volume
plus gravity force per unit volume.
, i.e. mass per
unit volume times acceleration equals pressure force per unit volume
plus gravity force per unit volume.
- In this question you need to write that in Eulerian form first
to give the Euler equations. Compare with the equations in the
appendices in the back of the book.
- Now substitute the ideal stagnation point as discussed in
class into your Euler equations, and verify that the Euler
equations contain the same acceleration vector as the Lagrangian
solution already discussed in class.
- Then compute the pressure field (Eulerian) from these Euler
equations. Make sure you do that properly, as discussed in class.
Include gravity, producing a force per unit volume
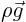 where the acceleration of gravity
where the acceleration of gravity 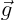 points down in the
minus
points down in the
minus 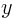 -direction. Compare the result with the Bernoulli law.
-direction. Compare the result with the Bernoulli law.
- Conversely, starting with the Bernoulli law, take minus the
gradient and verify that that gives the 2D Euler equations,
assuming that
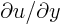 equals
equals
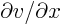 . (For ideal stagnation point flow, they
are both zero). In writing the Bernoulli law, you can assume that
the constant in it is the same for all streamlines.
. (For ideal stagnation point flow, they
are both zero). In writing the Bernoulli law, you can assume that
the constant in it is the same for all streamlines.
Hints: Note that the pressure is a scalar, not a vector. And that
you need to write it in terms of 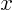 and
and 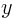 , to take the gradient.
The gradient of the pressure is a vector. The acceleration is the
Lagrangian time derivative of the particle velocity; read your
notes. In finding the pressure, put the solution of the first
equation into the second.
, to take the gradient.
The gradient of the pressure is a vector. The acceleration is the
Lagrangian time derivative of the particle velocity; read your
notes. In finding the pressure, put the solution of the first
equation into the second.
- If the surface temperature of a river is given by
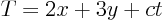 and the surface water flows with a speed
and the surface water flows with a speed 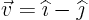 , then
what is
, then
what is 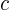 assuming that the water particles stay at the same
temperature? (Hint:
assuming that the water particles stay at the same
temperature? (Hint: 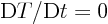 if the water particles
stay at the same temperature. Write this out mathematically in
Eulerian form.)
if the water particles
stay at the same temperature. Write this out mathematically in
Eulerian form.)
- A boat is cornering through this river such that its position is
given by
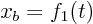 ,
, 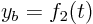 . What is the rate of change
. What is the rate of change
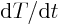 of the water temperature experienced by the boat in
terms of the functions
of the water temperature experienced by the boat in
terms of the functions 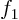 and
and 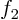 ?
?
![]() that moves over one free
path length
that moves over one free
path length ![]() . During that motion it will hit another
molecule if the center of the other molecule is within a radius
. During that motion it will hit another
molecule if the center of the other molecule is within a radius ![]() from the path of the molecule. In other words, the center of the
other molecule must be inside a cylinder of radius
from the path of the molecule. In other words, the center of the
other molecule must be inside a cylinder of radius ![]() around the
path
around the
path ![]() of the first molecule. There should be about one
collision in a free path, so there should be about one other
molecule within the cylinder. So the free path can be ballparked
from setting the volume of the cylinder equal to the average volume
per particle:
of the first molecule. There should be about one
collision in a free path, so there should be about one other
molecule within the cylinder. So the free path can be ballparked
from setting the volume of the cylinder equal to the average volume
per particle:
![]() can you no longer use the normal
(Navier-Stokes) equations to compute the flow at the
can you no longer use the normal
(Navier-Stokes) equations to compute the flow at the
![]() and
and ![]() , to take the gradient.
The gradient of the pressure is a vector. The acceleration is the
Lagrangian time derivative of the particle velocity; read your
notes. In finding the pressure, put the solution of the first
equation into the second.
, to take the gradient.
The gradient of the pressure is a vector. The acceleration is the
Lagrangian time derivative of the particle velocity; read your
notes. In finding the pressure, put the solution of the first
equation into the second.