6.1 Mixing layers:

$\begin{displaymath} \hbox{\epsffile{figures/mix.ps}} \end{displaymath}$

Consider a turbulent mixing layer (AKA shear or vortex layer) as shown above. Going downstream, you would expect the velocity profile to be of the generic functional form

$\begin{displaymath} \overline{u} = F(x,y,U_{\rm ave},\Delta U,\nu,\mbox{initial conditions}) \end{displaymath}$

where

is the horizontal distance from the starting point of the layer,

the vertical coordinate through the layer, $U_{\rm ave}$ the average of the velocities above and below the layer, and $\Delta U$ the velocity change over the layer.

However, in a free turbulent flow, away from walls, the laminar shear stress is small compared to the turbulent one. This suggests that the laminar viscosity $\nu$ can be ignored in the relation above. (Remember from the energy cascade discussion that the laminar stress is important in the dissipation of turbulent kinetic energy. But it should not be involved in the large-scale mechanics of the turbulent mixing layer, like the instability mechanisms that sustain the big eddies. If $\nu$ changes, it should only affect at which scales the energy cascade gets rid of its energy.)

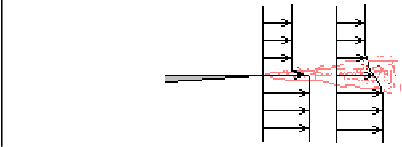
Also, if you look sufficiently far downstream, the details of the initial conditions should no longer be visible.

Dimensional analysis can now be done for the mean velocity profile $\overline{u}$ above. Selecting and $\Delta U$ to nondimensionalize the remaining variables gives

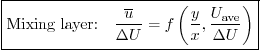
$\begin{displaymath} \fbox{$\displaystyle \mbox{Mixing layer:}\quad \frac{\ove... ... = f\left(\frac{y}{x},\frac{U_{\rm ave}}{\Delta U}\right) $} \end{displaymath}$

But the second argument of

above is a constant, independent of

for a given mixing layer. So it follows that the mixing layer velocity profile is similar, and that the layer has a typical thickness $\delta$ proportional to

Exercise:

Discuss how well that seems to agree with flow visualizations.

$\bullet$

Note that while in a boundary layer approximation the mixing layer can reasonably be approximated as relatively thin compared to its streamwise extend, this approximation does not improve with streamwise distance.