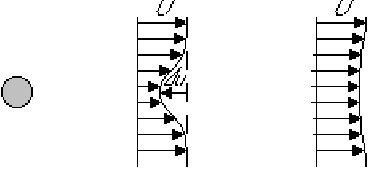
Finally consider the wake of some body, as shown above. Here you
would expect that downstream
Again,  can be ignored. Also, it can again be assumed that the
details of the initial conditions become invisible sufficiently far
downstream, with the exception that
can be ignored. Also, it can again be assumed that the
details of the initial conditions become invisible sufficiently far
downstream, with the exception that
cannot become invisible because it is constant. If 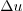 has
become small enough, we can expand the square and ignore the
has
become small enough, we can expand the square and ignore the  term to give that
term to give that
is constant. Since the first term is just a constant too, more simply
must be constant. In two dimensions this has units 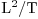 and in three
and in three  .
.
The functional relationship simplifies to
and dimensional analysis then gives
Because of the second argument of function 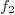 , there is little
useful knowledge that we can get from this.
, there is little
useful knowledge that we can get from this.
However, we can supplement the dimensional analysis with what we
believe to be true about the turbulence. Consider the two-dimensional
Reynolds-averaged  -momentum equation in boundary layer
approximation:
-momentum equation in boundary layer
approximation:
The average laminar stress should be negligible and when 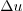 has become small enough compared to
has become small enough compared to  , we can also approximate the
left hand side to give
, we can also approximate the
left hand side to give
(Note that  should, based on continuity,
be of the same order as
should, based on continuity,
be of the same order as 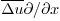 ,
hence negligible compared to the retained term.)
,
hence negligible compared to the retained term.)
If we ballpark the two sides in the simplified momentum equation
above,
or rearranged
In particular, there would be a problem in reasonably balancing the
momentum equation if 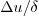 would be proportional to a
different power of
would be proportional to a
different power of  for large
for large  than
than 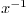 . In addition,
since
. In addition,
since 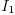 is constant, in two dimensions we also have the constraint
that
is constant, in two dimensions we also have the constraint
that 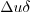 must stay of order
must stay of order 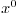 . Combining the two,
in two dimensions, as far as powers of
. Combining the two,
in two dimensions, as far as powers of  are concerned, we must have
that
are concerned, we must have
that
We can use that additional knowledge by recasting the previous
nondimensional relationship for 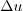 in terms of nondimensional
ratios that do not vary with
in terms of nondimensional
ratios that do not vary with  and a remaining one that does.
First, we can trivially rewrite the previous nondimensional
relationship as
and a remaining one that does.
First, we can trivially rewrite the previous nondimensional
relationship as
Here we have cleverly formed nondimensional combinations for
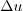 and
and 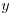 that should be independent of
that should be independent of  for large
for large  .
But the right hand side can be written as a different function
.
But the right hand side can be written as a different function 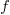 whose first argument is the nondimensional combination for
whose first argument is the nondimensional combination for 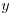 that
does not depend on
that
does not depend on  :
:
Function 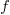 is not a new function, it is fully determined by
is not a new function, it is fully determined by 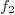 :
if you know the arguments of
:
if you know the arguments of 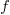 , you can compute those of
, you can compute those of 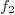 and
then
and
then 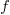 . But function
. But function 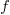 cannot depend on its second argument, or
else the shown nondimensional combinations for
cannot depend on its second argument, or
else the shown nondimensional combinations for 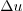 and
and 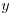 would not be independent of
would not be independent of  as they should.
as they should.
Cleaning up then gives
It may be noted that if substitute the above similar profile into the
simplified momentum equation above, assuming some suitable constant
eddy viscosity 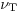 for the viscous term, you can find the
profile. You will get a reasonable approximation to the actual
measured wake velocity profile except near the outer edges. Note that
near the outer edges the flow is only part of the time truly
turbulent, as near the outer edges turbulent eddies engulf regions of
potential flow fluid. The
for the viscous term, you can find the
profile. You will get a reasonable approximation to the actual
measured wake velocity profile except near the outer edges. Note that
near the outer edges the flow is only part of the time truly
turbulent, as near the outer edges turbulent eddies engulf regions of
potential flow fluid. The intermittency
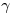 is
defined as the fraction of time that the flow is turbulent. It turns
out that if you assume that
is
defined as the fraction of time that the flow is turbulent. It turns
out that if you assume that 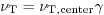 ,
with
,
with 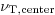 a suitable constant, you can get very good
agreement with the experimental profile.
a suitable constant, you can get very good
agreement with the experimental profile.
In three dimensions, accounting for the different 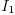 ,
,
Note that in this case, the Reynolds number based on 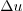 and
and
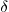 is proportional to
is proportional to 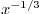 , so it decreases with
, so it decreases with  .
Therefore the made assumption of high Reynolds number will eventually
break down, and the wake will even become laminar. The result above
assumes that you do not look that far downstream. (The
two-dimensional wake above and the three-dimensional jet have Reynolds
numbers that stay constant with
.
Therefore the made assumption of high Reynolds number will eventually
break down, and the wake will even become laminar. The result above
assumes that you do not look that far downstream. (The
two-dimensional wake above and the three-dimensional jet have Reynolds
numbers that stay constant with  , so the approximation of high
Reynolds number, while qualitatively quite reasonable, does not
improve with
, so the approximation of high
Reynolds number, while qualitatively quite reasonable, does not
improve with  in those cases.)
in those cases.)
![]() can be ignored. Also, it can again be assumed that the
details of the initial conditions become invisible sufficiently far
downstream, with the exception that
can be ignored. Also, it can again be assumed that the
details of the initial conditions become invisible sufficiently far
downstream, with the exception that
![]() -momentum equation in boundary layer
approximation:
-momentum equation in boundary layer
approximation:
![]() in terms of nondimensional
ratios that do not vary with
in terms of nondimensional
ratios that do not vary with ![]() and a remaining one that does.
First, we can trivially rewrite the previous nondimensional
relationship as
and a remaining one that does.
First, we can trivially rewrite the previous nondimensional
relationship as
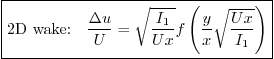
![]() for the viscous term, you can find the
profile. You will get a reasonable approximation to the actual
measured wake velocity profile except near the outer edges. Note that
near the outer edges the flow is only part of the time truly
turbulent, as near the outer edges turbulent eddies engulf regions of
potential flow fluid. The
for the viscous term, you can find the
profile. You will get a reasonable approximation to the actual
measured wake velocity profile except near the outer edges. Note that
near the outer edges the flow is only part of the time truly
turbulent, as near the outer edges turbulent eddies engulf regions of
potential flow fluid. The ![]() is
defined as the fraction of time that the flow is turbulent. It turns
out that if you assume that
is
defined as the fraction of time that the flow is turbulent. It turns
out that if you assume that ![]() ,
with
,
with ![]() a suitable constant, you can get very good
agreement with the experimental profile.
a suitable constant, you can get very good
agreement with the experimental profile.
![]() ,
,
![\begin{displaymath}
\fbox{$\displaystyle
\mbox{3D wake:}\quad
\frac{\Delta u}...
...x^2}}
f\left(\frac{y}{x}\sqrt[3]{\frac{Ux^2}{I_1}}\right)
$}
\end{displaymath}](img129.gif)