Viscous Flows

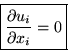
(Book 10.2, 3, 5)

Equations for viscous incompressible flows with constant density (these equations also apply to the flow of air at low Mach numbers, eg M<0.3:)

Continuity:

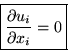
Momentum:

with .

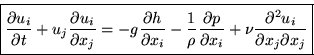
The gravity term can be eliminated by defining an artificial (kinetic) pressure

However, this does not work if there are free surfaces, since the boundary condition at the free surface would involve the true pressure, not the artificial one.

Differences in flows due to differences in scale can be taken into account by selecting a reference length L and a reference velocity V and then nondimensionalizing all variables with respect to these variables:

For example, for flow past a sphere, people typically normalize all lengths with the diameter of the sphere, L=D, and all velocities with the incoming stream V=U.

Scaled equations:

Continuity:

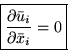
Momentum:

where Re is the nondimensional Reynolds number:

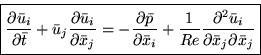
A necessary condition for two viscous flows around similar bodies to really be similar is that the Reynolds number is the same. Often there are other nondimensional numbers that also need to be the same due to boundary conditions (free surfaces), variable density effects, additional terms in the governing equations, etcetera.

Since is numerically quite small for fluids like water and air, we are typically interested in flows at high Reynolds numbers. Note that as far as the dimensional equations are concerned, a small viscosity has the same effect as a large Reynolds number.

04/05/00 0:13:20 04/05/00 0:22:39