Residue theorem

D'Alembert and Kutta-Joukowski only apply to bodies in an otherwise uniform stream. If there are other bodies or singularities (vortices, sources, ...) in the fluid, we need to actually integrate Blasius expression. This requires doing a complex contour integral.

We have already seen that the value of a complex contour integral depends on the singularities of f inside the contour: In fact, the quickest way to do this sort of integrals is usually to add the contributions of all the singularities together. These contributions are called the residues.

Let the function f have singularities at positions z=a₁, z=a₂. z=a₃, ... inside the contour:

The residues correspond to the integrals along small circles around the singular points:

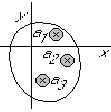
The total integral can be written:

There are two ways to find the residue at a singular point z=a_i:

1.

Use Taylor series expansions around the singular point z=a_i to write f as a Laurent series:

then

Note: To use the residue theorem, function f should only involve integer powers of . Broken powers, logarithms, ... are not acceptable.

2.

Use the following general formula:

where n is chosen just big enough so that the term within the square brackets is not singular at z=a_i.

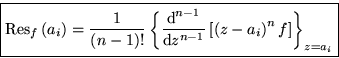
Exercise:

Evaluate along circles of radius r=1, 2, 3, ... around the origin. Use Taylor series expansions for the sin and cos to find the Laurent series for the cot.

Exercise:

Evaluate along circles of radius r=1, 2, 3, ... around the origin. Use the second method above.

As an example, the force on a Rankine body would be difficult to find by actual integration of the pressure. Using Blasius and the residue theorem, it is easy. The velocity potential is (uniform flow, source at z=0, sink at z=e:)

so the complex conjugate velocity is:

There are two singular points; one at z=0, the other at z=e. Blasius formula is:

Expanding W²:

To find the residue at z=0, we can look at each term separately. The first, third, and fifth term do not have a residue since they are not singular at z=0. The second term is a one-term Laurent series that does not have a 1/z term. The fourth term is a 1/z term with a coefficient (residue) . The residue of the sixth term can be found using the formula above with n=1; it is :

Similarly, at z=e the first, second, and fourth terms are not singular. The third term is a one-term Laurent series with no 1/(z-e) term. The fifth term has a residue , and the sixth has a residue :

Since the sum of the residues is zero, there is no net force.

Exercise:

Use Blasius and the residue theorem to find the forces on a cylinder in a uniform stream U that has a circulation . Compare with D'Alembert and Kutta-Joukowski.

03/24/00 0:30:56 03/27/00 0:16:52 03/27/00 0:31:25 03/31/00 0:02:09 03/31/00 0:06:20