Use the MacCormack scheme to compute the supersonic flow in a
constant area duct of height h. Assume that the nominal flow in
the duct is that of air expanded isentropically to a M=2 flow from
standard stagnation air (i.e. Mn=2, p0n=1 atm, T0n= 288
K, with corresponding pn and Tn at Mn=2, while un=Mn
an and vn=0.) Assume the actual flow at the entrance x=0 has
the same entropy and total enthalpy as the nominal flow, and v=0,
but the pressure is given by 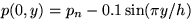 . Compute the flow downstream of the exit using the MacCormack scheme.
Use as many mesh points as the computer will take and plot the
deviations from nominal to clearly show its evolution.
. Compute the flow downstream of the exit using the MacCormack scheme.
Use as many mesh points as the computer will take and plot the
deviations from nominal to clearly show its evolution.
To find 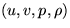 from
from 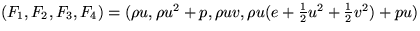 , first find
v as v=F3/F1. Next, noting that F2=F1 u + p and, with
, first find
v as v=F3/F1. Next, noting that F2=F1 u + p and, with
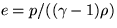 ,
, 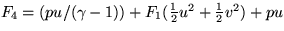 , we can eliminate p from these two expressions
to get a quadratcic equation for u with coefficients
, we can eliminate p from these two expressions
to get a quadratcic equation for u with coefficients 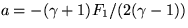 ,
, 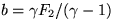 , and c = F1
v2/2. The roots are, using round-off insensitive expressions,
, and c = F1
v2/2. The roots are, using round-off insensitive expressions,
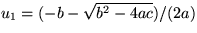 ; u2=c/(a u1). The root
u1 will be the one you want. Then
; u2=c/(a u1). The root
u1 will be the one you want. Then 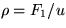 and
p=F2-F1 u. (Taken)
and
p=F2-F1 u. (Taken)
![]() from
from ![]() , first find
v as v=F3/F1. Next, noting that F2=F1 u + p and, with
, first find
v as v=F3/F1. Next, noting that F2=F1 u + p and, with
![]() ,
, ![]() , we can eliminate p from these two expressions
to get a quadratcic equation for u with coefficients
, we can eliminate p from these two expressions
to get a quadratcic equation for u with coefficients ![]() ,
, ![]() , and c = F1
v2/2. The roots are, using round-off insensitive expressions,
, and c = F1
v2/2. The roots are, using round-off insensitive expressions,
![]() ; u2=c/(a u1). The root
u1 will be the one you want. Then
; u2=c/(a u1). The root
u1 will be the one you want. Then ![]() and
p=F2-F1 u. (Taken)
and
p=F2-F1 u. (Taken)