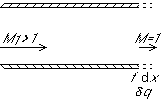
Next: Governing Equations Up: Choked! Previous: Choked!

Introduction

At this point, you are probably wondering what is so special about Mach 1 anyway? Why does the flow below;

entering the duct at a supersonic speed, gladly accept that we add heat to it inside the duct before the Mach number reaches unity, but if we try to add the tiniest amount of heat after that, it blasts a nasty shock wave upstream at us, turning the entire duct flow subsonic?

And it is the same if we try to add a bit of friction instead of heat beyond Mach one. Why does adding friction fail again precisely at Mach one?

Why does the subsonic flow below;

first accept us squeezing down on the narrow section without it changing the mass flow in the least, but when the Mach number in the narrow section reaches one, the mass flow suddenly starts dropping down proportional to the remaining narrow cross-sectional area? And why is it again at Mach one, not at say Mach two? (For a physical explanation of this particular case, instead of the current mathematical one, see elsewhere in the web lecture notes.)

Do such problems arise only for perfect gases, or maybe also for Van der Waals gases or experimental gases? And if so, is it again at Mach one for such gases, or at another Mach number?

Well, I want to convince you that it is not a coincidence, and not just for perfect gases. And that it is always Mach one.

Surprisingly, it all has to do with weak shocks propagating with the speed of sound, in other words, occurring at Mach one in a system in which the weak shock is steady.

Why would weak shocks at Mach one have anything to with, say, a Mach one flow refusing to provide a solution when a bit more heat is added? The rough answer is in a lesson from linear algebra: ``If a system of equations has multiple solutions, the system is singular and does not generally have a solution for an arbitrary right-hand side.'' Weak shocks are a nonunique solution, (there are two different flow states, the one before and the one after the shock), and so they indicate trouble.

We will now examine how this works precisely.

Next: Governing Equations Up: Choked! Previous: Choked!