Critical or Choked Flow
Charney Davy

In any flow the conservation equations much be satisfied. In the case of having a choked flow I will be paying particular attention to the mass conservation equation:

Assuming a constant area duct, the equation is reduced to

which can be rewritten as

By neglecting the higher order terms (because and are very small) we get:

dividing the equation by gives:

hence

The equation gives the relationship between the velocity and density, which tells us that the velocity is inversely proportional to the density, therefore, if the velocity increases the density decreases and vice versa.

Now in the case of a choked flow where M =1, in this case at the throat, the mass flow rate through the throat is constant. That is, once the reaches its threshold of M=1, no matter what changes take place upstream and downstream of the flow the mass flow rate will remain the same. The question is now how does the flow speed up? The answer to that goes back to mass conservation. In the previous equations I showed you that the density of a gas is inversely proportional to the velocity, . If you look closer at the conservation of momentum equation, you will also get another equation in terms of velocity and pressure,

In an accelerating isentropic flow, the pressure and density decrease while the velocity increases. The reason why changes in the back pressure p_b of the flow have no effect on the flow once M=1 is reached is because all pressure changes in the flow propagate in the nozzle at the speed of sound. Once the gas velocity reaches the speed of sound, M=1 at the throat, the effects of the changes cannot propagate up the nozzle since all the changes in the flow are traveling at the speed of sound (the same speed as the flow itself). Therefore once M=1 is reached at the throat; changes in the back pressure will not influence the flow in the nozzle and therefore cannot influence the mass flow rate through the nozzle. A converging-diverging nozzle is illustrated in figure 1 below.

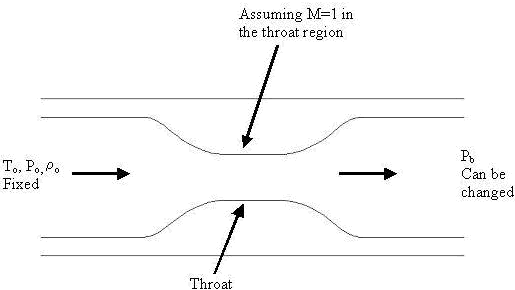
Instructor's Note: This was written by graduate student Charney Davy. The physical explanation why the flow no longer increases when the Mach number in the throat reaches unity is correct, though the relationship with the provided formulae, for a constant area duct, could have been made more clear.